Problemas de regiones en el plano complejo 1
Muestre que el conjunto:
Omega = {z que pertenece a C u|Re(z) - 4|+|Im(z) - 3|>= 2} es cerrado
1 Respuesta
Amo 1965!
Es equivalente a la gráfica de
|x-4|+|y-3| >=2
Se dan cuatro casos según los signos de los interiores. Si lo de dentro del valor absoluto es positivo se puede quitar y si es negativo hay que cambiarle el signo para quitarlo
a) x-4 +y -3>=2 ==> y >= -x +9 si x>=4, y >=3 superior
b) x-4-y+3 >=2 ==> y <= x -3 si x>=4, y < 3 inferior
c) -x+4+y-3>=2 ==> y >= x +1 si x <4, y >=3 superior
d) -x+4-y+3>=2 ==> y <=-x+5 si x<4, y<3 inferior
Se dibujan las rectas
y = -x + 9
y = x - 3
y = x + 1
y =-x + 5
y según las cuatro zonas que se forman con las rectas
y=3
x=4
En cada una de ellas dibujamos la parte superior o inferior a la recta que le corresponda.
Por ejemplo, en la zona superior derecha que es donde x>=4 , y >=3
la inecuación que le corresponde es
y>=-x+9
eso quiere decir que dibujaremos la parte superior a la recta y=-x+9 en esa primera zona.
Así se hace con las otras zonas y el resultado es este
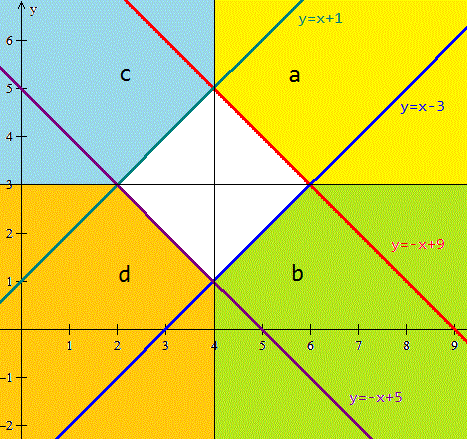
Las líneas están dentro del conjunto omega por tener >= en su definición
Y el complementario sería el blanco sin las líneas que es un abierto. Como el complementario es un abierto, entonces omega es un cerrado.
Y eso es todo.
No sé si te ha llegado la respuesta al ejercicio:
Graficar la frontera del conjunto:
omega = {z que pertenece a C u|Re(z)|> 1,|Im(z)|>=2}
Lo resolví y te mandé la respuesta pero no me aparece como enviado y si lo vuelvo a enviar me dice que no se puede mandar dos veces.
Si no te ha llegado. Vuelve a mandarme la pregunta para que la conteste con lo que tengo antes de apagar el ordenador.
