Calculo 3 derivadas parciales J

12)

Es como la copa de un cáliz flotando en el aire a 1 unidad métrica del suelo. Tiene 1 um de radio y sqrt(2)-1 de altura. Fuera de esa copa vale 0. En el borde de la copa también vale 0.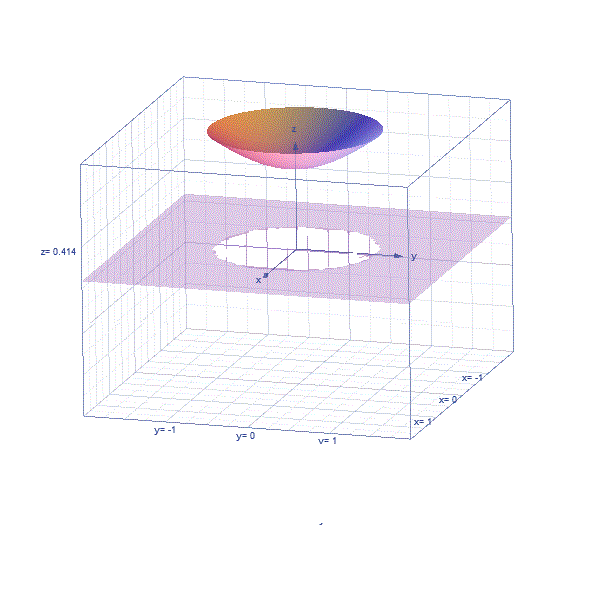b) Las derivadas parciales dentro de la copa son

fx(×,y) = ×/sqrt(×^2+y^2+1)

fy(×,y) = y/sqrt(×^2+y^2+1)

Me adelanto y calculo primero esta, que existe y es

fy(0,0)=0/sqrt(0^2+0^2+1) = 0/1 = 0

Ahora vamos con las complicadas

fx(0,1) = lim h->0 de [f(0+h,1)-f(0,1)] / h =

En el punto (0,1) la función vale 0 porque ×^2+y^2 = 0^2+1^2=1 >=1

lim h->0 de [f(h,1)-0]/h =

y como para todo h se cumple (0+h)^2+ 1^2 = 1+h^2 >=1 se cumple que f(h,1)=0

= lim h->0 de [0-0] / h

Y estos son los que hemos hecho varias veces y valen 0.  Luego

fx(0,1)=0

fy(1,0) = lim h->0 de [f(1,0+h)-f(1,0)] / h

Y aquí mismo despachamos ya este límite.

Como esta función cumple f(×, y)=f(y,×) podemos transformar este límite en exactamente el mismo que en la parte anterior y por lo tanto

fy(1,0)=0

Y eso es todo.