1 Respuesta
a) F(1/2, 1/2) = P(Y1 <= 1/2; Y2 <= 1/2)
La zona donde la probabilidad es no nula es
0<=y1<= 1
y1-1 <= y2 <= 1-y1
El límite inferior de y2 puede valer entre -1 y 0 el superior entre 1 y 0
Si lo limitamos a cuando y1 <= 1/2
El límite inferior puede valer entre -1 y -1/2 y el superior entre 1 y 1/2
Como el superior supera el valor máximo que puede tomar y2 como límite superior hay que poner 1/2
Es un pequeño lío creo. Mejor hacemos el dibujo. En amarillo los puntos donde Y1 e Y2 son menores que 1/2. Asi se ve claramente que el límite inferior de Y2 es y1-1 y el superior 1/2
$$\begin{align}&F(1/2,1/2)=\int_0^{1/2}\int_{y_1-1}^{1/2}30y_1y_2^2dy_2dy_1 =\\ &\\ &\\ &\int_0^{1/2}\left[ 10y_1y_2^3 \right]_{y_1-1}^{1/2}dy_1=\\ &\\ &\\ &\int_0^{1/2}10y_1\left(\frac 18-y_1^3+3y_1^2-3y_1+1\right)dy_1=\\ &\\ &\\ &\int_0^{1/2}\left(\frac{90}{8}y_1-10y_1^4+30y_1^3-30y_1^2\right)dy_1=\\ &\\ &\left[ \frac{90}{16}y_1^2-2y_1^5+\frac{30}{4}y_1^4-10y_1^3 \right]_0^{1/2}=\\ &\\ &\\ &\frac{90}{64}-\frac{2}{32}+\frac{30}{64}-\frac{10}{8}=\\ &\\ &\\ &\frac{90-4+30-80}{64}=\frac{36}{64}=\frac{9}{16}\end{align}$$Uff,
Uff que lío mi hice con las cuentas!
Tengo que dejarlo un momento largo, luego continuaré.
Se me había olvidado insertar el dibujo.
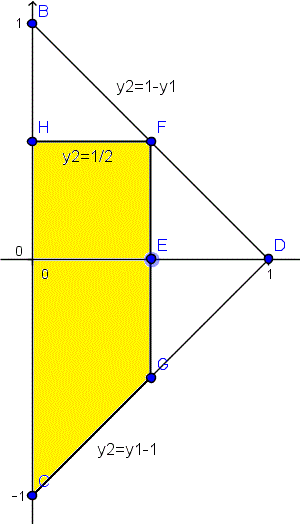
Corresponde a la parte a recién hecha
b) F(1/2, 2) = P(Y1<=1/2, Y2<=2)
Ahora Y2 debe ser menor que 2. Se nos fijamos en el dibujo, eso hace que el triangulito superior entre dentro de los valores validos. El límite inferior para Y2 será y1-1 y el superior 1-y1
$$\begin{align}&F(1/2,1/2)=\int_0^{1/2}\int_{y_1-1}^{1-y_1}30y_1y_2^2dy_2dy_1 =\\ &\\ &\\ &\int_0^{1/2}\left[ 10y_1y_2^3 \right]_{y_1-1}^{1-y_1}dy_1=\\ &\\ &\\ &\int_0^{1/2}10y_1\left(1-3y_1+3y_1^2-y_1^3 -y_1^3+3y_1^2-3y_1+1\right)dy_1=\\ &\\ &\\ &\int_0^{1/2}\left(20y_1-60y_1^2+60y_1^3-20y_1^4\right)dy_1=\\ &\\ &\\ &\\ &\left[10y_1^2-20y_1^3+15y_1^4-4y_1^5 \right]_0^{1/2}=\\ &\\ &\\ &\frac{10}{4}-\frac{20}{8}+\frac{15}{16}-\frac{4}{32}=\\ &\\ &\\ &\frac{80-80+30-4}{32}=\frac{26}{32}=\frac{13}{16}\end{align}$$c) P(Y1 >Y2)
En el dibujo trazamos la recta y2=y1. Pasa por (0,0) y el punto F del dibujo. Lo que está a la derecha cumple Y1>Y2. Lo más sencillo es restar de 1 el triangulito que queda encima de esa recta.
$$\begin{align}&P(Y1 \gt Y2)=1-\int_0^{1/2}\int_{y_1}^{1-y_1}30y_1y_2^2dy_2dy_1=\\ &\\ &\\ &1-\int_0^{1/2}10y_1\left[ y_2^3 \right]_{y_1}^{1-y_1}dy_1=\\ &\\ &\\ &\\ &1-\int_0^{1/2}10y_1(1-3y_1+3y_1^2-y_1^3-y_1^3)dy_1=\\ &\\ &\\ &1-\int_0^{1/2}(10y_1-30y_1^2+30y_1^3-20y_1^4)dy_1=\\ &\\ &\\ &1- \left[ 5y_1^2 -10y_1^3+\frac{30}{4}y_1^4-4y_1^5\right]_0^{1/2} =\\ &\\ &\\ &1 - \frac54 +\frac{10}{8}-\frac{30}{64}+\frac{4}{32}=\\ &\\ &\\ &\frac{64-80+80-30+8}{64}=42/64 =\frac{21}{32}=0.65625\end{align}$$Y eso es todo.
