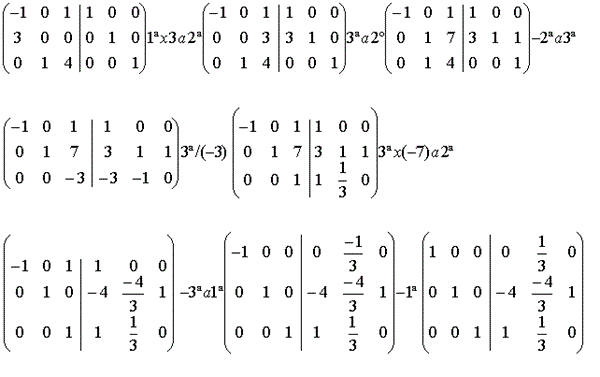Juan tq!
Es un proceso un poco tedioso, pero vamos.
Lo primero calcularemos el derterminante, porque si fuera cero no habría inversa
-1 0 1
3 0 0
0 1 4
|A| = 0 + 0 + 3 - 0 - 0 - 0 = 3
Ahora hay que construir la matriz de los adjuntos. El adjunto Aij = (-1)^(i+j) · alfaij
Donde alfa(i, j) es el menor complementario del elemento aij y su valor es el determinante de la matriz que queda quitando la fila i y la columna j.
Veamos alguno desarrollado:
A11 = (-1)^(1+1) · alfa11 = (-1)^2 · alfa11 = alfa11
donde alfa11 es el determinante de
|0 0|
|1 4|
que es 0 · 4 - 0 · 1 = 0. Luego A11 = alfa11 = 0
A12 = (-1)^(1+2) · alfa12 = (-1)^3 · alfa12 = -alfa12
|3 0|
|0 4|
que es 3 · 4 - 0 · 0 = 12. Luego A12 = -alfa12 = -1
Y es tedioso pero se tiene que hacer con todos y quedará:
0 -12 3
1 -4 1
0 3 0
Ahora hay que transponer esta matriz
0 1 0
-12 -4 3
3 1 0
y finalmente hay que dividir cada elemento por el determinante de la matriz que era 3
0 1/3 0-4 -4/3 1 1 1/3 0Pues ese es todo el proceso. En estudios superiores se enseña otra forma de hacerlo por sumas y productos simultáneos sobre la matriz y la identidad. Cuando conseguimos que la original se transforme en la identidad la otra se ha transformado en la inversa.
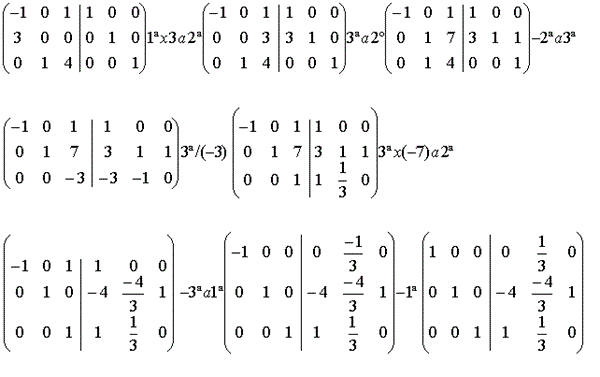
Y mientras la de la izquierda la hemos tranformado en la identidad la de la derecha se ha transformado en la inversa.
Entre medias de cada paso se explicaba la siguiente operación que se hace.
La primera fila multiplicada por 3 se suma a la segunda.
La tercera fila se suma a la segunda.
La segunda por (-1) se suma a la segunda
La tercera se divide por (-3)
La tercera por (-7) se suma a la segunda
La tercera se suma a la primera
La primera se muktiplica por (-1)
Y eso es todo. Si no lo has estudiado seguramente te obligarán a usar el primer método y no podrás beneficiarte del segundo, que lo bueno que tiene es que te acuerdas de él para toda la vida, mientras que el primero tuve que consultarlo y es trabajoso.