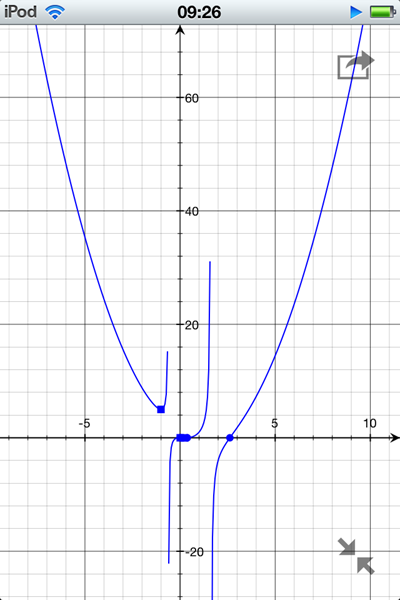
f(x) = (x^4 - 3x^3 + 2x^2) / (x^2 - x - 1)
Efectivamente, la división larga da:
x^2 - 2x + 1 + (- x + 1) / (x^2 - x - 1)
Lo primero será calcular los puntos donde se anula el denominador, eso nos dará las asíntotas verticales y los puntos donde no esta definida.
x= (1+-sqrt(1+4)) /2 = (1+-sqrt(5))/2
Asintotas:
x = (1-sqrt(5))/2
x = (1+sqrt(5))/2
Que expresadas en decimal para saber donde pintarlas son -0,6180339 y 1,618034
Otra cosa que se estudia también son los puntos de corte con el eje POR, en este caso serán los ceros del numerador:
x^4 - 3x^3 + 2x^2 = 0 ==> x = 0 es una raíz doble
Dividimos por x^2
x^2 - 3x + 2 = 0
x = 3+-sqrt(9-8)/2 = (3+-1/2) = 1 y 2
Luego los puntos de corte con el eje X son x=0, x=1 y x =2
Luego podemos hacer el análisis de signos. Hay que estudiar el signo en los intervalos delimitados por los ceros y por las asíntotas ya que en una asíntota puede haber un signo a un lado y otro al otro sin que haya habido un corte al eje por porque una asíntota es un punto de discontinuidad. Calcularemos el signo por la regla de los signos entre el signo del numerador y del denominador.
a) En (-infi, -0,6180339) Para por tendiendo a - infinito manda x^4 en el numerador y x^2 en el denominador luego signos positivos en ambos y signo + en el intervalo
b) En (-0,6180339, 0) El numerador aun no ha llegado a su primer cero luego positivo. El denominador ya paso su primer cero y cambió a negativo. Luego el signo (dado por numerador entre denominador) es negativo.
c) En (0, 1) Evaluamos el numerador porque el ser x=0 un cero doble no ha habido cambio de signo, pero eso tal vez sea un conocimiento de matemática superior. Por eso, evaluamos por ejemplo en x= 0,5 para que no quede duda
0,5^4 - 3·0,5^3 + 2·0,5^2 = 0,0625 - 0,375 + 0,5 = 0,1875
Efectivamente, no había cambiado el signo del numerador.
Luego el numerador es positivo y como el denominador sigue siendo negativo, la función es negativa.
d) En (1, 1,6180339) por fin cambio el signo del numerador tras atravesar un cero simple. De todas formas, lo confirmamos evaluando numerador en 1,5
1,5^4 - 3·1,5^3 + 2·1,5^2 = 5,0625 - 10,125 + 4,5 = -0,5625
El denominador sigue siendo negativo porque aun no pasó el segundo cero (de todas formas tu puedes evaluar los signos cuando quieras a tu manera). Y el signo de la función es positivo
e) En (1,6180339, 2) Acabamos de pasar una asíntota, mejor hacer tabla rasa y evaluamos el signo en 1,8 en numerador y denominador
1,8^4 - 3·1,8^3 + 2·1,8^2 = 10,4976 - 17,496 + 6,48 = - 0,5184
1,8^2 - 1,8 -1 = 0,44
Luego signo negativo
f) En (2, infinito) igual argumento que en a), si evaluamos en un punto muy grande predominan los términos de mayor grado de los polinomios que son positivos y el signo es positivo.
A tu gráfica le pasa lo siguiente. El punto de corte x = 2 está mal puesto, lo tienes en x = 2,6. No aparece la parte negativa entre 0 y 1, espequeña pero existe.


¿No sé qué más puedas necesitar? Dímelo si necesitas máximos, mínimos u otras cosas. Si no, puntúa para cerrar la pregunta.