Volumen de un solido, el ejercicio esta mal planteado o yo estoy mal
Tengo este ejercicio al realizar la gráfica noto que no existen puntos de intersección

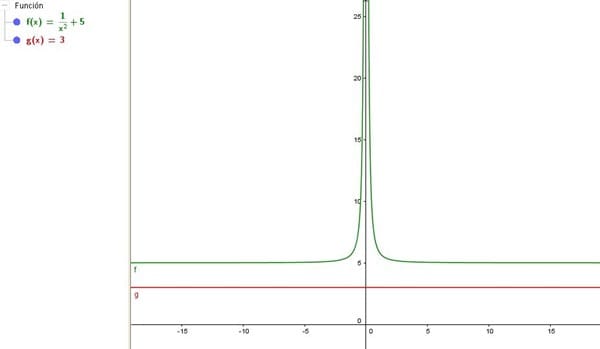
Me pueden explicar el ejercicio
2 Respuestas
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1
