Hacer la siguiente demostración
Sea C una circunferencia. Si una recta secante es paralela a una recta que contiene al diámetro D. Demostrar que la mediatriz de D es mediatriz también de la cuerda contenida en la recta secante.
1 Respuesta
Podemos mover y girar el conjunto formado por la circunferencia con sus cuerdas y mediatrices, eso no afecta a las distancias, paralelismos o perpendicularismos existentes.
Y lo que haremos será colocar la circunferencia centrada en (0,0) con la la cuerda del diámetro superpuesta al eje X.
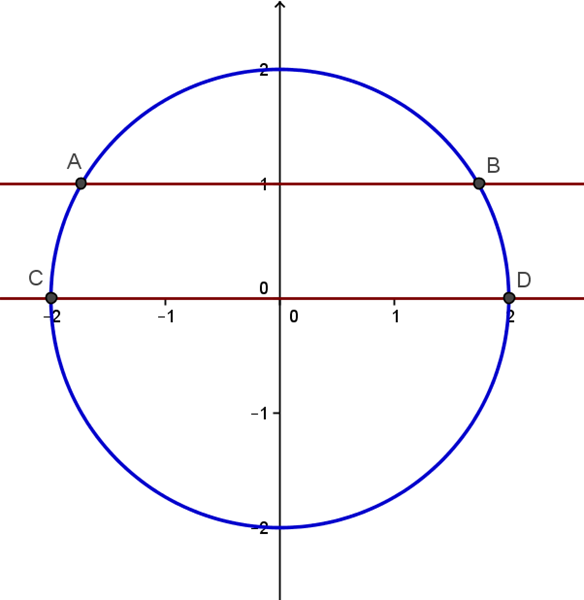
Entonces la otra cuerda por ser paralela, será un segmento horizontal y estará contenida en una recta de ecuación y=k para cierta k tal que 0 <= k <= R
La mediatriz de la cuerda que es el diámetro es la perpendicular al eje X pasando por el centro de la circunferencia, es decir, el eje Y. Vamos a demostrar que el eje Y también es la mediatriz de la cuerda AB.
El eje Y es perpendicular a AB ya que AB es paralelo a CD y todas las perpendiculares a la recta AB lo son a la recta CD.
La circunferencia es simétrica respecto el eje Y ya que su ecuación es
x^2 + y^2 = R^2
Entonces si el punto (x, y) verifica la ecuación también la verifica el punto (-x, y)
Por lo tanto A y B son simétricos respecto del eje Y y su distancia a él es la misma.
Luego el eje Y es perpendicular al segmento AB y la distancia de los puntos A y B a él es la misma, eso significa que el eje Y es la mediatriz de la cuerda AB.
Y eso es todo.
