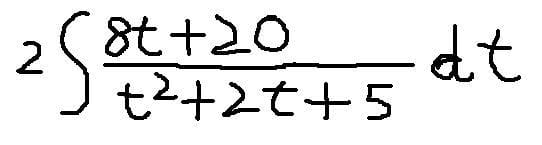Integral con polinomio en denominador

El polinomio del denominador tiene raíces complejas, por eso no se descompone en fracciones con denominadores más simples. Lo que pasa es que esa integral no es ni mucho menos directa.

Hay que descomponerla en suma de un logaritmo neperiano y un arcotangente. Puede ser que aparezcan las dos funciones o solo una.

Para la parte del logaritmo tendremos que hacer que el numerador sea la derivada del denominador salvo si acaso el producto por una constante y lo que quede deberá tener en el numerador solo un número y será la parte del arcotangente.

Veámoslo que se entenderá mejor. El 2 va a estar dando mal y puede olvidarse, mejor lo meto dentro

$(6t + 40)dt/(t^2+2t+5) =

La derivada del denominador es 2t+2, vamos a tomar un múltiplo de esto en el numerador de forma que tenga toda la parte de la t

entonces tomamos 3(2t+2) = 6t+6

Y descomponemos la integral en dos así

$(6t+6)dt/(t^2+2t+5) +$34dt/(t^2+2t+5)

La primera es

3ln|t^2+2t+5| por la forma que la hemos construido.

La segunda será un arcotangente. Ahí es donde se emplea lo del polinomio equivalente que decías

34$dt/[4+(t+1)^2] =

Y para que tenga forma de derivada de arcotangente hay que conseguir ponerlo como un 1 mas un cuadrado, se permiten constantes que multipliquen a todo para conseguir eso.

Se multiplica y divide por 4 el denominador. Es pesadísimo escribir con el editor de ecuaciones que hay incorporado en la página, pero lo usare para que lo veas claro

$$\begin{align}&=34 \int \frac{dt}{\frac{4(4+(t-1)^2)}{4}}= \frac{34}{4}\int \frac{dt}{1+\frac{(t-1)^2}{4}} =\\ &\\ &\\ &\\ &\frac{34}{4}\int \frac{dt}{1+ \left ( \frac{t+1}{2} \right )^2} = \frac{34}{4}2arctg \left ( \frac{t+1}{2} \right )\end{align}$$

Y la integral completa es:

3ln|t^2+2t+5| + 17 arctg[(t+1)/2] + C

Y eso es todo.

Creo que hay un fallo porque al principio cuando multiplicas el 2 de fuera por la integral, en numerador quedaría (16t+40), a no ser que haya algún tipo de simplificación k yo no vea..