Volumen de un tanque elíptico horizontal
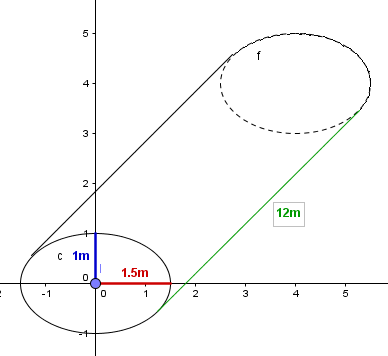
Tengo un tanque elíptico ubicado horizontalmente y quiero saber la formula para saber cuántos galones tiene, las medidas son:
Longitud 12 m
Radio corto 1m
Radio largo 1.50 m
Medida del combustible 90 cn
3 respuestas
Soy nuevo y esta es la primera vez que respondo aquí.
El área de una elipse viene dado por:
$$\begin{align}&A = \pi r_1r_2\end{align}$$El volumen de un tanque eliptico se calcula multiplicando el area de la elipce basal del tanque por la altura de este de la siguiente manera:
$$\begin{align}&V = \pi r_1 r_2h\end{align}$$Donde
R1 y r2 son los radios corto y largo. Como el producto es conmutativo no importa quien sea r1 y r2, lo importante es que ambos radios estén en la fórmula multiplicándose. H es la longitud o altura del tanque. Por tanto el volumen es:
$$\begin{align}&V = \pi (12m)(1m)(1.5m) =18 \pi m^3 = 56.55 (aprox)\end{align}$$El volumen en galones es :
$$\begin{align}&(56.55 m^3)\frac {1 galon }{0.00378541 m^3} = 1493893 galones \end{align}$$
·
·
¡Hola Luis Alfredo!
La fórmula del volumen del elipsoide es:
$$\begin{align}&V=\frac 43\pi abc\\&\\&\text{donde a,b,c son los tres semiejes, o radios}\\&\text{como los estás llamando.}\\&\\&\text{Nos das dos radios de 1m y 1.50 m}\\&\text{El otro es la mitad de la longitud}\\&c=\frac{12}2=6\\&\\&\text{Luego el volumen es}\\&V= \frac 43\pi·1\,·\,1.50\,·\,6= 12\pi\,m^3\approx \\&37.69911184m^3\\&\\&\text{Y lo convertimos a galones}\\&1m^3=264.172 galones\\&\\&V=37.69911184\,·\,264.172=9959.049774galones\\&\\&\text{O si no necesitas tanta precisión}\\&\\&V=9959 galones\end{align}$$:
:
Muchas gracias por su colaboración y si me sirve de mucho
Luis Alfredo!
Debes valorar la repuesta.
De todas formas tengo una duda con el lenguaje, lo mejor hubiera sido que adjuntaras una imagen o foto. Me parece que quieres de cir que la sección transversal es una elipse y no que tenga forma espacial de elipsoide (balón de rugby) como pensaba yo. Entonces es un tanque con sección elíptica y mucha altura y lo tienes lleno hasta 90 cm. El volumen sería este.
$$\begin{align}&\pi abh= \pi·1m·1.5m·0.9m = 1.35\pi\; m^3\approx\\&\\&4.24115 m^3=\\&\\&4.24115 · 264.172 = 1120.3931 galones\end{align}$$Yo creo que ahora si está resuelto como querías. No olvides valorar.
Saludos.
:
:
Vamos a ver. Lo que he hecho no está bien me parece. Al final llego a la conclusión de que el depósito está tumbado y que los cortes verticales producen una elipse. Pero necesito saber si el radio largo es a lo ancho a lo alto. Es decir, los 90 cm de altura del combustible son 90 cm del radio largo o del radio corto. Lo contestaré cuando pueda, es complicado de escribor sobre todo ¿necesitas la demostración o te conformas con el resultado?
¿Sería este el tanque?
Espero la aclaración.
Saludos.
:
:
Entiendo que el problema es algo más complicado; tal como yo lo veo, el tanque está parcialmente lleno hasta una altura de 90 cm. Y no creo que se trate de un elipsoide, sino de un tanque usual de sección transversal elíptica.