Área entre curvas, calculo integral

·

·

¡Hola Juan Lopez!

Debemos hallar los extremos de la región que delimitan las curvas, al ser polinomios de grado 2 se espera 2 respuestas y sería una región simple.

Esta es la gráfica.

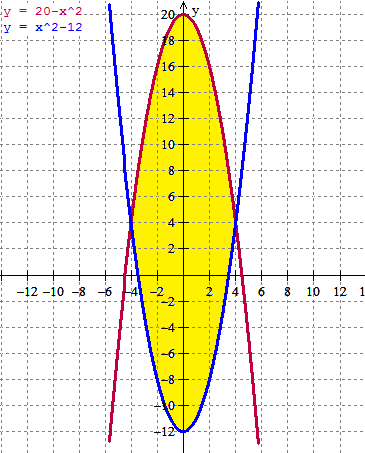
Se ve claramente que los puntos de intersección son (-4,4) y (4,4)  no obstante vamos a comprobarlo numéricamente.

y=20-(-4)^2= 20-16 = 4

y= x^2-12 =(-4)^2-12)=4

Luego (-4, 4) es intersección de ambas

y= 20-4^2 = 4

y=4^2-12 = 4

Luego (4,4) también es punto de intersección.

Y el área será la integral entre - 4 y 4 de la diferencia de las ds funciones. Como sabemos que la roja es la superior la pondremos de minuendo.

$$\begin{align}&A=\int_{-4}^4\left[20-x^2-(x^2-12)  \right]dx=\\&\\&\int_{-4}^4(20-x^2-x^2+12) dx=\\&\\&\int_{-4}^4(32-2x^2)dx=\\&\\&\left[32x-\frac{2x^3}{3}  \right]_{-4}^4=128-\frac{128}{3}+128-\frac {128}{3}=\\&\\&256-\frac{256}3= \frac{2·256}{3}= \frac {512}3\\&\\&\text{Menos lío de signos si hubieramos usado que es simetrica}\\&\\&A=2\left[32x-\frac{2x^3}{3}  \right]_{0}^4=2\left(128-\frac {128}3  \right)=2·\frac{256}3=\frac {512}{3}\end{align}$$

:

:

Para que lo. Necesitass