Calcular valor ángulo por altura correspondientes a los lados
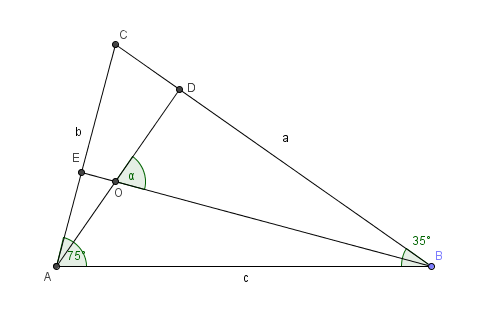
El problema dice lo siguiente :En un triágulo "ABC" se sabe que los angulos "A" = 75º y "B" = 35º. Calcular el valor del ángulo determinado por las alturas correspondiente a los lados ( a ) y ( b).
Pregunto cómo se calcula, porque si lo tengo que calcular por ángulos interiores de un triángulo me queda C= 180º-75º-35º, lo que me da un valor de 70º.
Si en cambio sumo "A" + " B" = 75º + 35º = 110º,que es el resultado que da el problema.
La verdad he estado viendo este tema pero no se como desarrollarlo, envío una imagen que hice yo porque no sale la figura del triángulo y puede ser cualquiera.
1 respuesta
·
·
¡Hola Hfarias!
Haré un dibujo exacto de lo que piden.
El triángulo ABE es rectángulo. Por lo tanto el ángulo ABO = 90º-75º=15º
El triángulo BAD es rectángulo, luego BAO = 90º-35º= 55º
Entonces el ángulo AOB = 180º-15º-55º = 110º
Pero se llama ángulo definido por dos rectas al menor de ellos, el que he llamado alfa en el dibujo, alfa es el suplementario de AOB
alfa = 180º-110º = 70º
Luego la respuesta correcta es 70º, si el libro te dice 110º está equivocado porque debe ser el menor de los dos ángulos, a nos ser que se especifique y te pidan el mayor de los dos.
:
:
¡Gracias! Amigo Valeron es la primera vez que este tipo de problema en los triángulos, se puede calcular por medio de la fórmula de héron los lados si cónosco los ángulos.
Ó existe alguna fórmula en especial.
Gracias
La fórmula de Heron te da el área del triangulo conociendo las longitudes de los lados, luego no sirve para este caso.
Si conoces los tres ángulos (o dos porque eso lleva al tercero) y no conoces ningún lado no puedes dar las longitudes de los lados ya que hay infinitos triángulos con los mismos ángulos pero unos más grandes que otros . Lo que sí obtendrás es una fórmula que relaciones las longitudes de los lados, mediante el teorema de los senos.
Y eso es todo, saludos.
:
:
