Tengo una duda con estas demostraciones de probabilidad
no se como comenzar disculpen tantas molestias. Espero gratamente sus respuestas
1 Respuesta
·
39)
Uno de los axiomas que debe cumplir un espacio probabilístico es que la probabilidad de la unión de sucesos mutuamente excluyentes es la suma de las probabilidades de los sucesos.
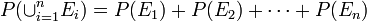
para todo conjunto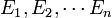 
de sucesos disjuntos, es decir, tales que: 
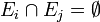para todo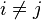 
Al ser A_i una partición las intersecciones A_i ∩ A_j =Ø para todo i, j.
Como A_i ∩ B incluido o igual a A_i
las intersecciones (A_i ∩ B) ∩ (A_j ∩ B) incluidas en A_i∩A_j=Ø
Luego los conjuntos del enunciado son mutuamente excluyentes y por lo tanto la probabilidad de su unión es la suma de la suma delas probabilidades.
·
41)
El otro ejercicio es el principio de inclusión-exclusión, sobradamente conocido y tiene que tener la demostración en varios sitios y seguramente es una demostación muy costosa de escribir aquí.
No creas que hay demostración completa en todos los sitios y en muchos dan solo la versión para el cardinal de conjuntos y no para la probabilidad.
Aquí tienes un sitio con la demostración completa pero hay otros que te a lo mejor te gustan más
http://repositorio.uis.edu.co/jspui/bitstream/123456789/7179/2/134780.pdf
Y eso es todo.
