Repaso de vectores

1) Calculemos el ángulo que forman los dos vectores.

Llamaré u al vector de 1000 unidades y v al de 3000 unidades. Si completamos el paralelogramo y llamamos A al punto donde termina u, B al punto de la circunferencia, C al punto donde termina v y D al que falta. Desde A tendremos el lado AB que mide 1000 y el lado horizontal AD que mide 3000. El ángulo interno del paralelogramo en A es theta ya que es el ángulo correspondiente a theta por una recta paralela. Y el vector suma es la diagonal BD.

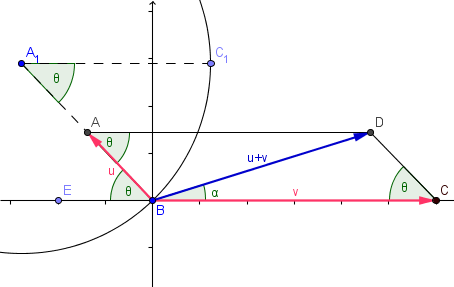
Se ha formado un triángulo ABD en el que aplicaremos el teorema de los cosenos para calcular BD

|BD|^2 = |AB|^2 + |AD|^2 - 2|AB||AD|cos(theta)

|BD|^2 = 1.000.000 + 9.000.000 - 6.000.000cos(theta)

|BD| = sqrt(10.000.000 - 6.000.000cos(theta))

|BD| = 1000·sqrt(10-6cos(theta))

Para calcular la dirección debemos calcular el ángulo alfa, lo haremos usando el teorema de los senos

|DC| / sen(alfa) = |BD| / sen(theta)

sen(alfa) = |DC| sen(theta) / |BD| = 1000sen(theta) / [1000·sqrt(10-6cos(theta))]

sen(alfa) = sen(theta) / sqrt(10-6cos(theta))

alfa = arcsen[sen(theta) / sqrt(10-6cos(theta))]

2) El vector u es

u = (1000cos(180-theta), 1000 sen(180-theta))

u = (-1000·cos(theta) , 1000·sen(theta))

Y el vector v es

(3000,0)

La suma es

(3000-1000 cos(theta), 1000sen(theta))

El módulo de la suma es

|u+v| = sqrt([3000-1000·cos(theta)]^2+ [1000sen(theta)]^2) =

sqrt[9000000 + 1000000cos^2(theta) -6000000·cos(theta) + 1000000sen^2(theta)]=

tenemos 1000000[cos^2(theta)+sen^2(theta)] = 1000000

sqrt[9000000 +1000000 - 6000000·cos(theta)] =

1000sqrt[10-6cos(theta)]

Y la dirección es

alfa = arctg{1000sen(theta) / [3000-1000 cos(theta)]} =

acrtg{sen(theta) / [3-cos(theta)]}

si tga = x

sena / cosa = x

sen^2(a) / cos^2(a) = x^2

sen^2(a) / [1-sen^2(a)] = x^2

sen^2(a) = x^2 - x^2·sen^2(a)

sen^2(a) + x^2·sen^2(a) = x^2

sen^2(a) = x^2 / (1+x^2)

sena = x / sqrt(1+x^2)

luego si tg(alfa) = sen(theta) / [3-cos(theta)]

$$\begin{align}&sen\alpha=\frac{\frac{sen\theta}{3-\cos\theta}}{\sqrt{1+\left( \frac{sen\theta}{3-\cos\theta}\right)^2}}=\\ &\\ &\\ &\\ &\frac{\frac{sen\theta}{3-\cos\theta}}{\sqrt{\frac{(3-\cos\theta)^2+sen^2\theta}{(3-\cos\theta)^2}}} =\\ &\\ &\\ &\frac{sen\theta}{\sqrt{(3-\cos\theta)^2+sen^2\theta}} =\\ &\\ &\\ &\frac{sen\theta}{\sqrt{9 +\cos^2\theta-6cos\theta +sen^2\theta}} =\\ &\\ &\\ &\frac{sen\theta}{\sqrt{10 -6cos\theta }}\\ &\\ &\\ &\\ &\alpha = arcsen \left(\frac{sen\theta}{\sqrt{10 -6cos\theta }}\right)\end{align}$$

Como vemos es lo mismo que se calculó por el otro método

c) Recuerdo que |u+v| =1000sqrt[10-6cos(theta)]

Si theta = 0

|u+v| = 1000·sqrt(10-6) = 2000

alfa = arcsen[0/sqrt(10-6)] = arcsen 0 = 0

en efecto es un vector horizontal de longitud 2000 lo que sale gráficamente

Si theta = 90

|u+v| = 1000·sqrt(10)

alfa = arcsen[1/sqrt(10)] = 18.43494882º

Es un cuadrado de lados 1000 y 3000, la diagonal mide 1000·sqrt(10) por el teorema de Pitágoras. El ángulo es el que corresponde a una tangente de 1000/3000 = 1/3

y se comprueba que arctg(1/3) = 18.43494882º

Si theta = 180º

|u+v| = 1000 sqrt(10+6) = 4000

alfa = arcsen[0/sqrt(10+6)] = arcsen 0 = 0

En efecto, son dos vectores horizontales hacia la derecha luego se sumas y da 4000