Ayuda con vectores

Pues vamos a hacer la demostración más vectorial posible. Es que cuando piden un determinado tipo de demostración habría que tener delante el capítulo del libro para ver como quieren que lo hagamos.

Los puntos A, B, C, D y los intermedios van a ser vectores, vectores con origen en el punto (0,0) y que terminan en A(a1, a2), B(b1, b2), etc.

El vector que va al punto intermedio de dos vectores es su semisuma

F=(A+B)/2

I =(A+D)/2

etc

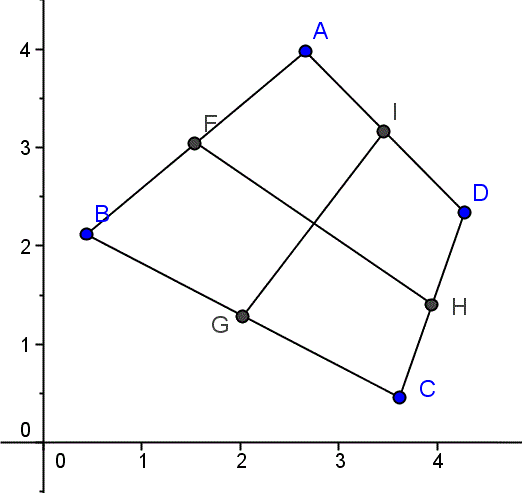
Y la ecuación de una recta es un punto más un vector por un parámetro. Vamos a hallar las ecuaciones vectoriales de las rectas que contienen los segmentos FH e IG, recordemos que esos cuatro puntos son intermedios, se pueden expresar como semisuma de los vértices. Y como vector de la recta tomaré el que une puntos intermedios.

recta FH: (A+B)/2 + [(C+D)/2 - (A+B)/2]t

recta IG: (A+D)/2 + [(B+C)/2 - (A+D)/2]s

Y ahora hallamos la intersección.

(A+B)/2 + [(C+D)/2 - (A+B)/2]t = (A+D)/2 + [(B+C)/2 - (A+D)/2]s

Esto podría ser un poco lioso, pero sabiendo cual va a ser la solución y con algo de lógica vamos a ver que si tomamos t=s=1/2 se cumple la ecuación vectorial

(A+B)/2 + [(C+D)/2 - (A+B)/2](1/2) = (A+D)/2 + [(B+C)/2 - (A+D)/2](1/2)

(A+B)/2 + (C+D)/4 - (A+B)/2 = (A+D)/2 + (B+C)/4 -(A+D)/4

(A+B)/4 + (C+D)/4 = (A+D)/4 +(B+C)/4

(A+B+C+D)/4 = (A+D+B+C)/4

Luego el punto de intersección se obtiene tomando t=s=1/2.

Pero t y s multiplican a los vectores que unen puntos intermedios. Si tomamos t=s=1/2 el punto que obtenemos es el punto medio de esos segmentos. Dicho de otro modo, los segmentos se bisecan entre sí.

Y eso es todo.