No hay cosa más complicada para mi que hacer los diagramas estos de comunicación.
Del 1 se puede pasar al 2 y 4
Del 2 al 1 y al 4
Del 3 al 1 y al 4
Del 4 al 1 al 3
Se puede pasar de
1 al 2, 2 al 4, 4 al 3, 3 al 1
Se cumple el ciclo de permutaciones (1,2,4,3) y con eso se puede llegar desde cualquiera a cualquiera.
Luego hay una única clase de comunicación {1,2,3,4}
Será mejor hacer el dibujo.
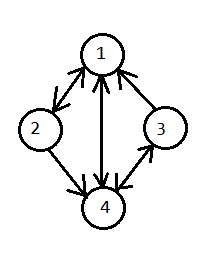
Todos los estados son recurrentes, se puede regresar a ellos siempre ya que siempre hay un camino que comunica cualquier punto con cualquiera.
Además también lo dice el corolario 2.2
En una cadena de Markov irreducible con espacio de estados finito, todos los estados son recurrentes. Y esta es una cadena irreducible por tener una sola clase de comunicación.
Al estado 1 se puede volver así:
1--> 2--> 1
1 --> 2 --> 4 --> 1
en la primera se vuelve en 2 pasos y en la segunda en 3.
El periodo es el máximo común divisor de los pasos en que se puede volver, luego en este caso el periodo es mcd(2,3) = 1
Al estado 2 se puede volver
2--->4--->1--->3
2--->4--->3--->1---->2
mcd(3,4)=1
Al 3 se puede volver en
3--->1--->4--->3
3--->1--->2--->4--->3
mcd(3,4)=1
Y al 4
4--->1--->4
4--->3--->1--->4
mcd(2,3) =1
Luego todos tiene periodo 1, son aperiódicos.
Y eso es todo.


