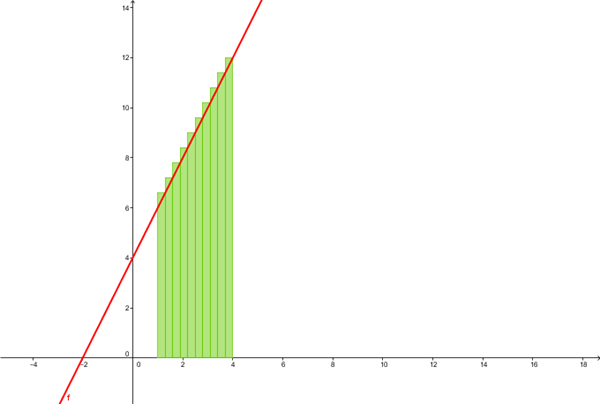
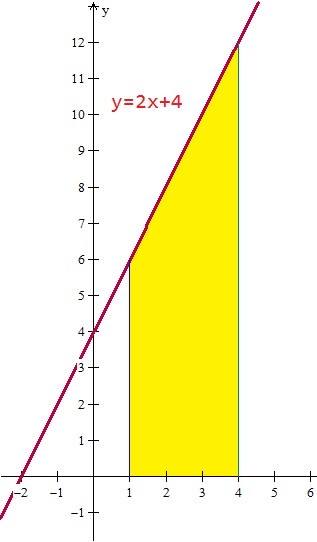
Sumas de Riemann (2) f(x) = 2x + 4 en el intervalo (1,4)
f(x) = 2x + 4 en el intervalo (1,4)
a) Evaluar la suma de Riemann escribiendo paso a paso el cómo la realizaste.
b) Traza la gráfica de la función en los intervalos establecidos.
2 respuestas
Siguiendo el mismo proceso que en el otro ejercicio:
$$\begin{align}&f(x)=2x+4\\&\\&\Delta x =\frac{b-a}{n}=\frac{4-1}{n}=\frac{3}{n}\\&\\&x_i=a+i·\Delta x=1+\frac{3i}{n}\\&\\&La \ n-esima \ suma \ de \ Riemann\\&\sum _{i=1}^{n}f(x_i)· \Delta x=\sum _{i=1}^{n}f(1+\frac{3i}{n})·\frac{3}{n}=\\&\\&\sum _{i=1}^{n} \left[2 \left( 1+\frac{3i}{n} \right) +4 \right]·\frac{3}{n}=\\&\\&\sum _{i=1}^{n} \left(6+\frac{6i}{n} \right)·\frac{3}{n}=\\&\\& \frac{3}{n} \left( \sum _{i=1}^{n}6+ \frac{6}{n} \sum _{i=1}^{n} i \right)=\\&\\&\frac{3}{n} \left( 6n+ \frac{6}{n}· \frac{n(n+1)}{2} \right)=\\&\\&\frac{3}{n} \left[ 6n+3(n+1) \right]=\frac{27n+9}{n}\\&\\&Suma \ Riemann:\\&\\&\lim_{n \to \infty}\frac{27n+9}{n}=27\\&\\&\end{align}$$
Falta votar esta
·
Dividimos el intervalo en n partes. Como la longitud es 3, cada intervalo tendrá longitud
3/n
Y la suma Riemann es el sumatorio de los n intervalos por el valor de la función en cada uno de ellos, en concreto haré la suma con los valores del extremo izquierdo.
$$\begin{align}&S_n=\sum_{i=0}^{n-1}\frac 3n\left(2\left(1+i·\frac 3n\right)+4 \right)=\\&\\&\frac 3n \sum_{i=0}^{n-1}\left(2+\frac{6i}{n}+4 \right)=\\&\\&\frac 3n \sum_{i=0}^{n-1}\left(6+\frac{6i}{n} \right)=\\&\\&\frac 3n \left(6n+\frac 6n\sum_{i=0}^{n-1}i \right)=\\&\\&18+\frac{18}{n^2}\sum_{i=0}^{n-1}i=\\&\\&\text{por la fórmula de la suma de sucesiones aritméticas}\\&\\&18+ \frac{18}{n^2}\frac{(n-1)n}{2}=\\&\\&18+ 9· \frac{n^2-n}{n^2}=\\&\\&18+9-\frac 9n =\\&\\&27 - \frac 9n\end{align}$$Y la suma Riemann es el límite cuando n tiende a infinito, con lo cual 9/n tiende a cero.
Luego la suma Riemann es 27.
Vamos a verificarlo haciendo la integral que es
x^2 + 4x entre 1 y 4
4^2 + 4·4 - 1 - 4·1 = 16+16 -1 -4 = 27
Luego está bien hecha.
·
Y esta es la gráfica.
Y eso es todo.