Hola ! ¿Me explican este problema? La ecuación demanda para un producto monopolista
La ecuación de demanda para el producto de u monopolista es p = 400-2 q, y la función de costos totales es C(q)= 0.2q^2 +4q +400, en donde q= numero de unidades p =precio en dolares.
a) Interpreta económicamente, la pendiente de la ecuación demanda. Calcula el ángulo de inclinación .
b) Graficar C(q)
c) Calcular la función utilidad .Determinar el nivel de producción en donde se maximizan las utilidades y el precio del producto. Calcular las utilidades máximas.
d) ¿Para qué nivel de producción hay ganancia? ¿Para cuáles perdida?
1 respuesta
a)
La ecuación de la demanda es una recta, y la pendiente de una recta puesta en la forma
y = ax + b
es el coeficiente a de la variable independiente
En la ecuación de la demanda la y es o y la x es q.
p = -2q + 400
La pendiente es -2
Li interpretación es que la recta es decreciente, a mayor cantidad producida menor es el precio por unidad.
La pendiente de una recta es la tangente del ángulo que forma dicha recta con el semieje OX
$$\alpha=tg^{-1}(-2)= -63.43494882º$$No sé si habrás dado que la función inversa de la tangente se llama arcotangente
alfa = arctg(-2)
En otros sitios lo verás escrito como atan, arctan y mil inventos.
b)
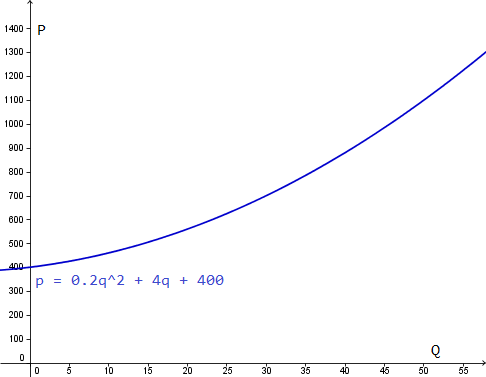
c)
La función utilidad son los ingresos menos los gastos.
U(q) = q(400-2q) - (0.2q^2 +4q +400) =
400q - 2q^2 - 0.2q^2 - 4q - 400 =
-2.2q^2 + 396q - 400
Para calcular el máximo se deriva e iguala a cero
U '(q) = -4.4 q + 396 = 0
-4.4q + 396 = 0
4.4q = 396
q = 396 / 4.4 = 90
La utilidad máxima se obtiene para q = 90 unidades
El precio del producto entonces cuando la utilidad es máxima es
p(90) = 400-2·90 = 400-180 = 220
y la utilidad máxima es
U(90) = -2.2 · 90^2 + 396 · 90 - 400 = 17420
d) Calcularemos los ceros de la función utilidad
-2.2q^2 + 396q - 400 = 0
2.2q^2 - 396q + 400 = 0
$$\begin{align}&q=\frac{396\pm \sqrt{396^2-4·2.2·400}}{4.4}=\\ &\\ &\frac{396 \pm \sqrt{153296}}{4.4}=\frac{396\pm391.53033}{4.4}=\\ &\\ &1.015833891 \quad y\quad 178.9841\end{align}$$Nótese que la función de la utilidad es una parábola invertida porque el coeficiente de q^2 es negativo, tiene forma de copa puesta hacia abajo. Entonces es positiva entre los puntos que cortan al eje X y negativa por los extremos de estos.
Entonces hay utilidad positiva entre
1.0158 y 178.9841
Y negativa entre
0 y 1.0158 y entre 178.9841 e infinito
No sé si el producto admite unidades fraccionarias, si no las admite
Utilidad positiva [2, 178]
Utilidad negativa [0, 1] U [179, infinito]
Y eso es todo.
