Centro de masa de un cardiode

Perdona por la tardanza, pero es que me han mandado algunos ejercicios bastante difíciles de los que se llevan casi todo el día. Y este tampoco era sencillo como para resolverlo de inmediato.

Un cardiode es una figura cerrada algo parecida a un corazón por es se llama así, lo mejor es dibujarlo y lo entenderás.

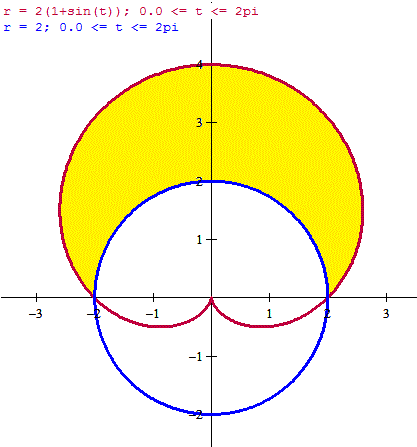
La figura roja es el cardiode, la azul la circunferencia y nos piden hallar el centro de masas de la figura que he pintado en amarillo. Sobre la coordenada x del centro de masas no haremos ninguna cuenta, la figura es simétrica respecto al eje Y y por tanto el centro de masas tiene coordenada x=0.

Para la coordenada y hay que resolver una integral, la fórmula dice

$$y=\frac{\int_cy\,dm}{\int_cdm}$$

Lo que pas es que la integral de arriba esta preparada para funciones expresables en coordenadas cartesianas, mientras que el cardiode no nos lo dan en cartesianas y es difícil expresarlo en ellas.

Tendremos que hacer un cambio de variables de cartesiana a polares. En polares usare las variables r y t, la r para el radio y la t para el ángulo, asi podemos hacer cuentas aquí sin poner letras griegas.

El cambio de variable de cartesianas a polares es

x = r·cost

y = r·sent

el jacobiano del cambio es, usando & como símbolo de las derivadas parciales

| &x/&r  &x/&t|   |cost  -r·sent|
|             | = |             |  =
| &y/&r  &y/&t|   |sent   r·cost|

r·cos^2(t) + r sen^2(t) = r

J = r

la integral que sea debe multiplicarase por este jacobioano al resolverla

Primero calculamos la integral del denominador. Vemos que la superficie amarilla tiene coordenadas polares para el ángulo entre 0 y pi y el radio entre las funciones r=a y r=(a(1+sent)

$$\begin{align}&m=\int_Cdm=\\ &\\ &\text{Sea }\gamma \text{ la densidad}\\ &\\ &=\int_{area}\gamma dS=\\ &\\ &\\ &\gamma\int\int_{area}dxdy =\\ &\\ &\gamma\int_0^{\pi}\int_a^{a(1+sent)}r\,dr\,dt=\\ &\\ &\gamma \int_0^{\pi}\left[\frac{r^2}{2}\right]_a^{a(1+sent)}dt=\\ &\\ &\gamma\int_0^{\pi}\left(\frac{a^2(1+sent)^2}{2}-\frac{a^2}{2}\right)dt=\\ &\\ &\frac{\gamma a^2}{2}\int_0^{\pi}(sen^2t+2sent)dt=\\ &\\ &Como \quad sen^2t=\frac{1-\cos\,2t}{2}\\ &\\ &=\frac{\gamma a^2}{2}\int_0^{\pi} \left(\frac{1-\cos\,2t}{2}+2sent\right)dt=\\ &\\ &\frac{\gamma a^2}{2}\left[\frac t2-\frac{sen\, 2t}{4}-2cost  \right]_0^{\pi}=\\ &\\ &\frac{\gamma a^2}{2} \left(\frac {\pi}2-0+2-0+0+2\right)=\\ &\\ &\frac{\gamma a^2(\pi+8)}{4}\end{align}$$

Y ahora la del numerador, la diferencia es la la integral tiene una y que debe ser sustituida por su espresión equivalente en coordenadas polares que es x = r·sent

$$\begin{align}&\int_Cydm=\\ &\\ &\text{Sea }\gamma \text{ la densidad}\\ &\\ &=\int_{area}\gamma xdS=\\ &\\ &\\ &\gamma\int\int_{area}y\,dx\,dy =\\ &\\ &\gamma\int_0^{\pi}\int_a^{a(1+sent)}r·r·sent\,dr\,dt=\\ &\\ &\gamma \int_0^{\pi}sent\left[\frac{r^3}{3}\right]_a^{a(1+sent)}dt=\\ &\\ &\gamma\int_0^{\pi}sent\left(\frac{a^3(1+sent)^3}{3}-\frac{a^3}{3}\right)dt=\\ &\\ &\frac{\gamma a^3}{3}\int_0^{\pi}(sen^4t+3sen^3t+3sen^2t)dt=\\ &\\ &Como \quad sen^2t=\frac{1-\cos\,2t}{2}\implies\\ &\\ &sen^4t=\frac{1-2cos2t+\cos^22t}{4}=\frac{2-4cos2t+1+cos4t}{8}=\\ &\\ &\frac{3-4cos2t+cos4t}{8}\\ &\\ &=\frac{\gamma a^3}{3}\int_0^{\pi}(3sen^3t)dt+\frac{\gamma a^3}{3}\int_0^{\pi}\left(\frac{3-4cos2t+cos4t}{8}+ \frac{3-3cos2t}{2}\right)dt=\\ &\\ &=\frac{\gamma a^3}{3}\int_0^{\pi}3(1-\cos^2t)sent\,dt+\\ &\\ &+\frac{\gamma a^3}{3}\int_0^{\pi}\left(\frac{15-16cos2t+cos4t}{8}\right)dt=\\ &\\ &\text{hacemos cambio de variable para la primera}\\ &z=-cost \quad dz = sent\,dt\\ &t=0\implies z=-1\\ &t=\pi\implies z=1\\ &\\ &\frac{\gamma a^3}{3}\left(\int_{-1}^{1}3(1-z^2)dz+\left[\frac{15t}{8}-sen\,2t+\frac{sen\,4t}{32}\right]_0^{\pi}\right)=\\ &\\ &\frac{\gamma a^3}{3}\left(3\left[z-\frac{z^3}{3}  \right]_{-1}^1+\frac{15\pi}{8}-0+0-0+0-0  \right)=\\ &\\ &\frac{\gamma a^3}{3}\left(3-1+3-1+\frac{15\pi}{8}  \right)=\\ &\\ &\frac{\gamma a^3}{24}\left( 32+15\pi \right)\end{align}$$

Y ya solo queda hacer el cociente

$$\begin{align}&y=\frac{\frac{\gamma a^3}{24}\left( 32+15\pi \right)}{\frac{\gamma a^2(\pi+8)}{4}}=\frac {a(32+15\pi)}{6(8+\pi)}\\ &\\ &\text{vamos a aproximarlo}\\ &\\ &y = 1.1836113a\end{align}$$

No parece mal, en nuestro dibujo, como a= 2, el centro de masas estaría en

(0, 2.3672226)

Que ya digo que es muy posible

Bueno, pues el centro de masas tiene coordenada x=0 y la cooordenada y es lo que pone arriba, que no puedo escribir más porque el ordenador ya no puede con tantas fórmulas y se va a colgar.

Y eso es todo.