El lugar geométrico serán los puntos que cumplen las condiciones que nos piden, es decir que sus distancias a los dos brazos tengan la proporción m/n. Dicho lugar puede ser un punto, dos puntos, una recta, una circunferencia, parábola o lo que sea. Una vez hallado intentaremos averiguarlo.
Vamos a poner coordenadas cartesianas de la manera más cómoda posible para operar.
El punto O sera el (0,0) el punto A será (m, 0), es decir el brazo OA será el eje X+ y el punto B será (n·cosw, n·senw) donde w es el ángulo antihorario que forma el brazo OB con el eje X+.
PUede verse que OB = sqrt[(n^2)cos^2(w) + (n^2)sen^2(w)] =
= n· sqrt[cos^2(w)+sen^2(w)] = n
La recta definida por O y B es
y = x·tgw
y - x·tgw = 0
multiplicando por cosw
ycosw - xsenw = 0
Y la distancia de un punto (x, y) a esta recta es:
d = |ycosw -xsenw| / sqrt [cos^2(w) + sen^2(w)] = |ycosw -xsenw|
La distancia de cualquier punto (x,y) al brazo AB es simplemente |y|
Estas distancias son porporcionales a m/n de esta forma
|y| / |ycosw - xsenw| = m/n
n|y| = m|ycosw - xsenw|
Si signo(y) = signo(ycosw - x senw) tenemos
ny = mycosw -mx senw
ny - mycosw = -mx senw
y(n - mcosw) = -mx senw
y = mxsenw / (mcosw - n)
Si signo(y) distinto signo(ycosw - x senw) tenemos
ny = -mycosw + mx senw
ny + mycosw = mx senw
y (n + mcosw) = mx senw
y = mxsenw / (mcosw +n)
Luego tenemos que el lugar geométrico son dos rectas pasando por el origen con ecuaciones:
y = mxsenw / (mcosw - n)
y = mxsenw / (mcosw +n)
Geométricamente puede que lo entendamos mejor:
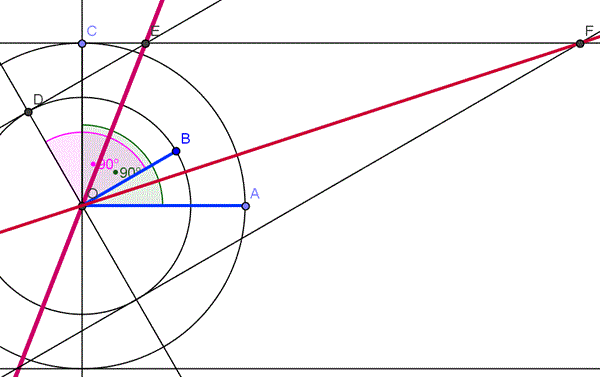
Se comienza construyendo Los brazos OA y OB. Trazamos lasperpendiculares OC y OD trasladando además las distancias OA y OB con compás. Trazamos paralela a OA por C y paralela a OB por D. Estas rectas paralelas cumplen que tiene distancia constante a los brazos que es preciasamente la longitud del los brazos. Donde se corten que es E tendremos un punto a distancia m de OA y distancia n de OB, que es lo que buscamos. El lugar geométrico es la recta que tiene esta punto y el origen.
La otra recta se obitiene como intersección de la otra parelela a distancia n de OB pero por la parte de abajo con la paralela a OA. Nos da un punto F y OF es la otra recta del lugar geométrico.
Y eso es todo.


