Sobre rectas y vectores
hola vale ,pido disculpa por que en la anterior pregunta le di solo 3 estrellas , debieron ser mas , yo siempre le he dado altas puntuaciones a excepción de la ultima ,es que ese problema casi me vuelve loco de no poder desarrollarlo .Ahora en adelante puntuare maximamente .
si me pudiera ayudar con este pequeño ejercicio es el # 2
http://www.subeimagenes.com/img/img004-518828.html
un saludo
1 Respuesta
Acepto las disculpas. Pero ponte de mi lado. El problema era muy complicado, el dibujo ese me costó mucho tiempo hacerlo y no salían las cuentas por ningún lado. Después de todo eso me doy cuenta que se me había olvidado poner un dato que lo hubiese facilitado. ¿Y qué voy a hacer con todo lo que había hecho? Hay preguntas que no se tendrían que puntuar con 5 no con 10 sino con 50 o más. Y entonces veo que después de todo el trabajo no estás dispuesto a dar 5 puntillos de propina. Pues se te quitan las ganas de responder preguntas de esas tan complicadas y te dedicas a disfrutar de la vida.
Ya me dirás que curso estás estudiando, es posible que sea más alto que el que llegué yo a estudiar. Y ten un poco de paciencia para recibir la respuesta que la pregunta lleva bastante trabajo, usar el programa Geogebra para hacer el dibujo no es tan simple.
descuida vale , entiendo ..
y esos problemas son del curso de matemática basica
Este es el dibujo. El cuadrado era tan grande que no aparece todo porque entonces n se vería el triángulo con detalle. Puse KH=10 es lo mismo que HI=10 del enunciado porque es un cuadrado.
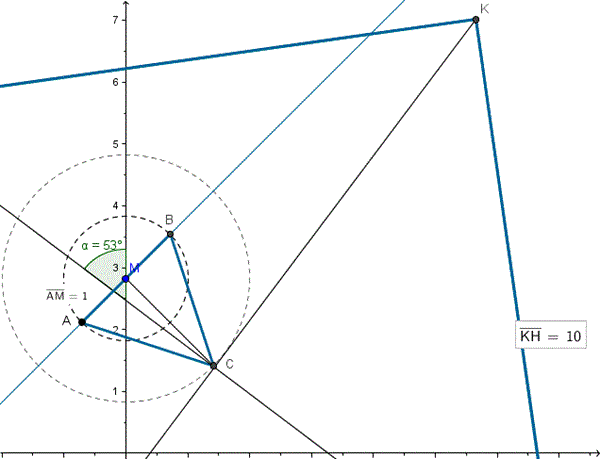
Si la proyección ortogonal en AB es el vector (1,1) significa que la recta AB forma 45ª con el eje X. El punto C está en la perpendicular a la recta AB que pasa por M ya que la distancia de C a A y B es la misma y M es el punto medio. Luego MC forma -45º con el eje X y el punto C será
C = M + 2(sqrt(2)/2, -sqrt(2)/2) =
(0, 2sqrt(2)) + (sqrt(2), -sqrt(2))
C = (sqrt(2), sqrt(2))
Y los puntos A y B están situados a distancia 1 de M sobre una recta de 45º, luego son
A = (0, 2sqrt(2)) + (-sqrt(2)/2, -sqrt(2)/2)
A = (-sqrt(2)/2, (3/2)sqrt(2))
B = (0, 2sqrt(2)) + (sqrt(2)/2, sqrt(2)/2)
B = (sqrt(2)/2, (5/2)sqrt(2)/2)
Para calcular los puntos HIJK tomaremos el punto C y le sumaremos los vectores de las mitades de las diagonales
Primero calculamos cuánto mide esa mitad de la diagonal
Si en un cuadrado el lado mide 10 tomamos 5 y eso será un cateto de un ángulo de 45º luego la hipotenusa medirá
5 / [sqrt(2)/2)] = 10/sqrt(2) = 10sqrt(2)/2 = 5sqrt(2)
Eso es lo que mide la mitad de la diagonal.
Un vector de modulo m y angulo a es
m(Cosa, sena)
Eso es lo que sumaremos adecuadamente al punto C para obtener los vértices.
Comenzamos por el punto que se ve el K, el ángulo que forma la diagonal es 53º
K = C + 5sqrt(2)(cos53º, sen53º)
K = (sqrt(2), sqrt(2)) + 5sqrt(2)(cos53º, sen53º)
K = sqrt(2)(1+5cos53º, 1+5sen53º)
Para el punto H que hay abajo el vector forma 90-53= 37º con el eje X
H = sqrt(2)(1+5cos37º, 1-5sen37º)
Para el punto I es
I = sqrt(2)(1-5cos53º, 1-5sen53º)
y para el J
J = sqrt(2)(1-5cos37º, 1+5sen37º)
Y eso es todo.
