Dada la siguiente ecuación obtener la ecuación en forma canónica de la correspondiente elipse

;)
Hola Karla!
Completando cuadrados:

$$\begin{align}&(x^2+6x)+(4y^2+16y)+21=0\\&\\&(x^2+6x)+4(y^2+4y)+21=0\\&\\&\text{esos binomios provienen de los siquientes cuadrados}:\\&x^2+6x=(x+3)^2-9\\&\\&y^2+4y=(y+2)^2-4\\&\text{la elipse queda:}\\&\\&(x+3)^2-9+4 \Big[(y+2)^2-4\Big]+21=0\\&\\&(x+3)^2+4(y+2)^2-4=0\\&\\&(x+3)^2+4(y+2)^2=4\\&\\&Dividiendo\ entre º 4\\&\\&\frac{(x+3)^2} 4+ \frac{(y+2)^2} 1=1\\&\\&\text{elípse horizontal, eje mayor en la fracción de lasX}\\&a=2\\&b=1\\&Centro(-3,-2)\\&Vértices\ eje \ mayor:\\&(-3+a,-2)=(-1,-2)\\&(-3-a,-2)=(-5,-2)\\&\text{Vértices eje menor}:\\&(-3,-2+b)=(-3,-1)\\&(-3,-2-b)=(-3,-3)\\&\\&Semidistancia \focal\\&a^2=b^2+c^2\\&\\&c^2=a^2-b^2\\&c^2=4-1=3\\&c= \sqrt 3\\&\\&Focos:\\&(-3+c,-2)=(-3+ \sqrt 3 , -2)\\&(-3-c,-2)=(-3-\sqrt 3,-2)\end{align}$$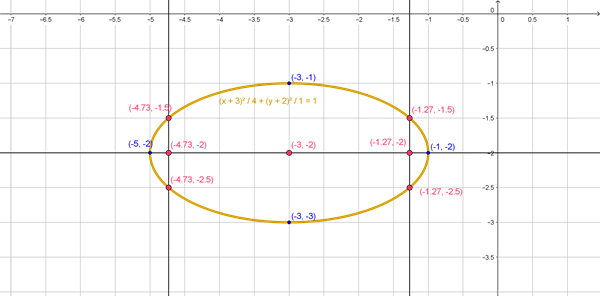

El lado recto del foco de la derecha se encuentra en la recta :

x=

$$\begin{align}&x=-3+ \sqrt 3\\&\\&\frac{(x+3)^2} 4+ \frac{(y+2)^2} 1=1\\&\\&\frac{(-3+ \sqrt 3+3)^2} 4+ \frac{(y+2)^2} 1=1\\&\\&\frac 3 4+ \frac{(y+2)^2} 1=1\\&\\& \frac{(y+2)^2} 1=1- \frac 3 4= \frac 1 4\\&\\&==>\\&y+2= +\frac 1 2\ \ ==>y= \frac 1 2 - 2=- \frac 3 2 ==> P=(-3+ \sqrt 3\ , - \frac 3 2)\\&\\&y+2= -\frac 1 2\ \ ==>y= -\frac 1 2 - 2=- \frac 5 2 ==> P'=(-3+ \sqrt 3 ,\ - \frac 5 2)\\&\\&\text{En el foco de la izquierda, y por simetría}:\\&Q=(-3 -\sqrt 3 \ ,\ - \frac 3 2)\\&Q'=(-3- \sqrt 3 \ ,\ - \frac 5 2)\end{align}$$

Saludos

;)

;)