Problemas de calculo integral: Encuentre el área de la región delimitada por las gráficas de las funciones y=x^3 Y y= 2x-x^2 .
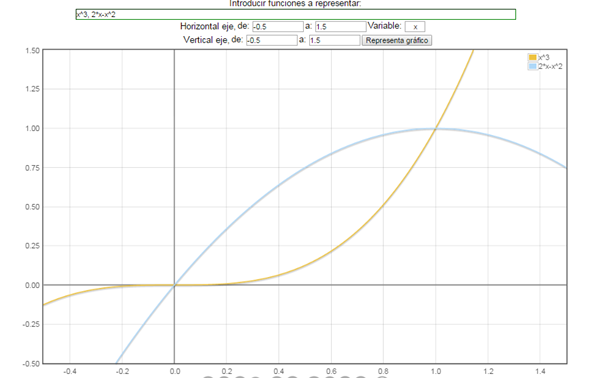
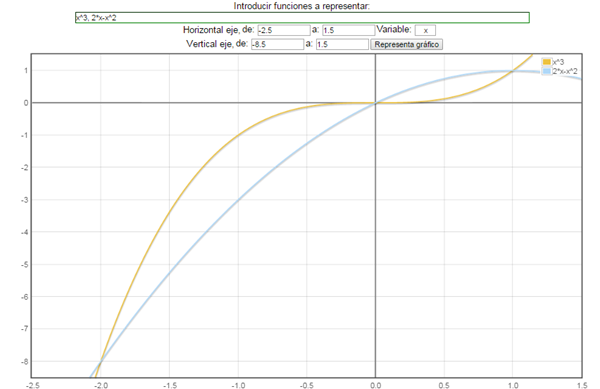
1 Encuentre el área de la región delimitada por las gráficas de las funciones y=x^3 Y y= 2x-x^2 . El área se expresa en unidades de superficie.
Sugerencia: Elabore la gráfica para una mejor comprensión del ejercicio.
2 La región limitada por la gráfica de y=x^3, el eje x y x=1/2 se gira alrededor del eje x. Hallar el área de la superficie lateral del sólido resultante.
Tener en cuenta que: El área lateral (excluyendo los extremos) del sólido resultante es:
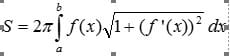
1 Respuesta
Respuesta
1