Se desea construir cajas metálicas sin tapa de volumen máximo con láminas cuadradas, que tienen 12 cm. Por lado recortándole...
Razón de Cambio
Se desea construir cajas metálicas sin tapa de volumen máximo con láminas cuadradas, que tienen 12 cm. Por lado recortándole cuadros iguales en las esquinas y doblando hacia arriba como lo muestra la figura:
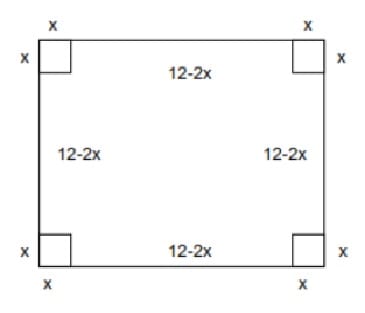
Sea x el lado del cuadrado que se va a recortar y V el volumen de la caja resultante, entonces
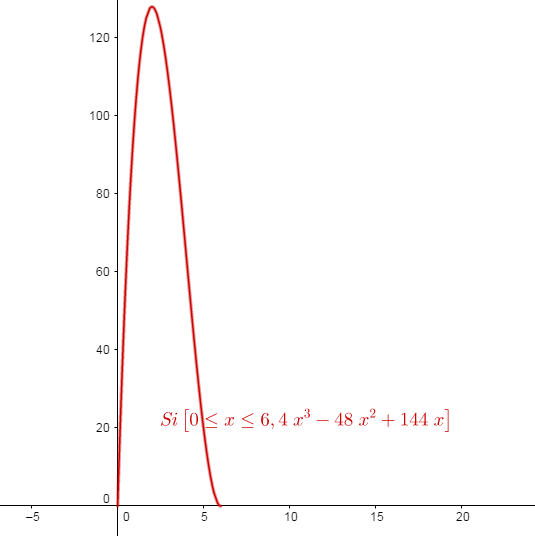
$$\begin{align}&f(x)=x(12-2x)(12-2x)=4x^3-48x^2+144x\end{align}$$Esboza la gráfica de esta situación
¿Cuánto mide cada lado x de los lados que se recortaran y cuál es el volumen máximo de la caja?
1 Respuesta
Si bien esa función es una cúbica que está definido para todos los reales, por el problema en sí, solo tiene sentido para valores de x entre 0 y 6. Te dejo la gráfica
Se ve que entre los valores hay un máximo, ahora vamos a calcularlo, derivando la función
f'(x) = 12x^2 - 96x + 144
f'(x) = 0 mediante la resolución de la cuadrática tenemos los valores:
x = 2
X = 6 es el extremo del intervalo, así que no sirve... igual verifiquemos mediante la derivada segunda
f''(x) = 24x - 96
f''(2) = -48 < 0 Máximo
f''(6) = 48 > 0 Mínimo
el volumen máximo será f(2) = 4 * 2^3 - 48 * 2^2 + 144 * 2 = 128
Salu2