¿De que se encargar una asociación de cáncer?

·

·

¡Hola Monik!

¿Ese es todo el enunciado?

Pues felicita de mi parte al que lo ha escrito. NO he visto enunciado más disparatado en toda mi vida. No es raro en los ejercicios de la prepa, pero en este se han sobrado. Supongo que detrás de todo esto habrá un profesor que entienda y se dará cuenta del despropósito de ejercicio que es.

Algunos detalles:

1) -X2 + 20 x no es una ecuación, falta al menos un signo igual y la parte derecha.

2) Si no fuese una ecuación sino una función nos están diciendo que la función es la misma que la variable independiente ya que no se habla de otra cosa que del número de tapas.

3) Si sustituimos 60000 en la función no da un número negativo... ¿Qué sentido tiene eso?

Yo creo que debes hablar con el profesor y comentarle esto para que dé la corrección que necesita el enunciado.

Espero la aclaración.

Saludos.

:

:

Vamos a hacer el enunciado bueno que creo yo, debe ser:

Una asociación contra el cáncer de niños se encarga de recolectar tapas de refrescos desechables con el propósito de venderlas y así obtener una cantidad de dinero extra para continuar con su labor.

Según su estadística, la función que representa el número de miles de tapas que se recolectan por unidad de tiempo es la siguiente f(x) =–x^2 + 20x, donde x señala el tiempo. Ligado a esto, la asociación ya cuenta con 60,000 tapas que ha recolectado por su cuenta.

Consultad alguno a ver si ese es el enunciado que debería ser. Tampoco todos porque se sospecharían algo.

Yo creo que ese sería el enunciado correcto a tenor de las preguntas que hacen después, ahora bien, a lo mejor no lo reconocen.

Espero noticias.

:

:

La página va fatal, no se actualiza, lo que acabo de escribir hace ya vario minutos no puedo verlo, espero que vosotros sí lo hayáis podido ver. Decía que la función f(x)=-x^2+20x es el número de miles de tapas que se recogen por unidad de tiempo (por ejemplo días sería una unidad muy aceptable) y la x es el tiempo en esa misma unidad de tiempo.

La función f(x) no es el número de tapas que hay en total sino las que se recogen diariamente, solamente así tiene algo de sentido el problema.

El bosquejo de la gráfica yo no lo puedo hacer a mano, vosotros sí y además deberéis hacerlo tal como os hayan enseñado que yo no sé como ha sido.

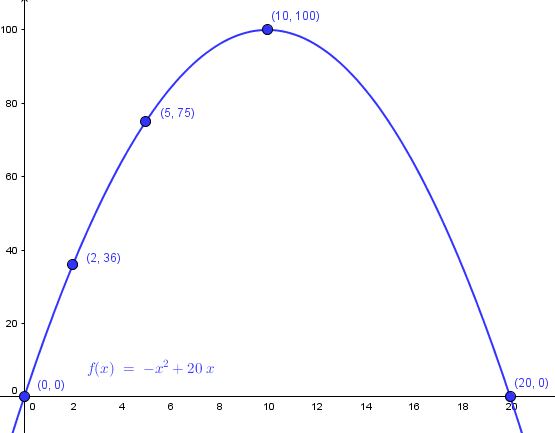
La función es una parábola hacia abajo por ser negativo el coeficiente de x^2.

Sería interesante conocer los cortes con el eje X:

-x^2 + 20 x = 0

x(-x+20)= 0

ya tenemos una solución x=0, y la otra sale de

-x+ 20 =0 

x=20

Luego los cortes son en 0 y 20.

Otro punto importante es el vértice de la parábola que en este caso será el máximo.

Esto se soluciona de dos formas, bien sabiendo la fórmula del vértice que es

x=-b/2a

O con teoría de máximos y mínimos.

De la primera forma es:

x= -20 / [2·(-1)] = -20 / (-2) = 10

De la segunda forma derivamos e igualamos a 0

f'(x) = -2x +20 = 0

-2x = -20

x = 10

Como puedes ver es el mismo vértice.

Y el valor de la función el el vértice es:

f(10) = -10^2 + 20·10 = -100 + 200 = 100

Luego el vértice es punto (10, 100)

Y aparte de esto podéis usar una tabla con los valores que estiméis oportunos, por ejemplo

2 ----> -2^2 + 20·2 = -4 + 40 = 36

5 ----> -5^5 + 20·5 = -25 + 100 = 75

...

calculáis los puntos que queráis en el intervalo [0, 20]

·

Las respuestas ya las he calculado para poder hacer la gráfica, luego a lo mejor querían que hicierais la gráfica solo con la tabla de valores y después dierais las respuestas que salen en la gráfica. La verdad es que a mí siempre me enseñaron que era al revés, se calculaban cortes con los ejes y máximos antes de hacer la gráfica.

De cualquier modo las respuestas son:

2a) Cuando más tapas se recolectan es en el tiempo 10 (días por ejemplo) se recolectan 100 miles de tapas, 100000 tapas.

Y ya no se recolecta nada en el tiempo 20.

2b) La relación entre el tiempo y el número de tapas recolectadas será una función. Como la función f(x) que tenemos es la del número de tapas que se recogen diariamente (suponiendo el día como unidad de tiempo), el número de tapas recogidas hasta el día x será la integral de f(x)

$$\begin{align}&g(x) = \int f(x)dx=\int(-x^2+20x)dt=\\&\\&-\frac{x^3}{3}+10x^2+C\\&\\&\text{Ahora hay que calcular C para que g(0) sea 60 miles}\\&\\&g(0) = C = 60\\&\\&\text{luego la función tapas recogidas hasta el tiempo x es}\\&\\&g(x) = -\frac{x^3}{3}+10x^2+60\\&\end{align}$$

3)

Ya estamos otra vez con otra pregunta incompleta, la recta secante ¿por qué puntos? Pero es que además se habrán confundido como otras veces y querrán decir la recta tangente, pero tampoco dicen por qué punto.

Yo me ofrecería a revisar todos los enunciados de los problemas que os mandan, porque es que vaya enunciados os ponen muchas veces.

Y eso es todo de momento mientras no se aclaren más las cosas.

Saludos.

.

:

Ya me he dado cuenta que han vuelto a confundir la palabra secante con la tangente, lo mismo que en el ejercicio del jitomate. Para que el enunciado sea correcto debería ser: hallar la ecuación de la recta tangente en el punto donde se alcanza el máximo de tapas recogidas diariamente, y no hallar la secante en no sé sabe dónde que es lo que dicen.

Ya sabemos que los máximos o mínimos relativos de una función derivable en un intervalo se alcanzan en los puntos críticos, donde la derivada es 0. Pero por la forma que preguntan quieren que uséis la fórmula de la ecuación de la recta tangente:

$$\begin{align}&y = y_0 + f'(x)(x-xo)\\&x_0=10\\&y_0=f(x_0)= -10^2 + 20·10 = -100 + 200 = 100\\&f'(x) = -2x +20\\&f'(x_0)=f'(10)= -2·10 + 20 = 0\\&\text{como ya había dicho antes, por lo tanto la recta es}\\&y= 100 + 0·(x-10)\\&y=100\end{align}$$

esa es la ecuación de la recta tangente, como veis es una recta horizontal.
Y entonces la gráfica en Geogebra es esta y podéis descargarla aquí: Tapas contra el cancer gráfica Geogebra

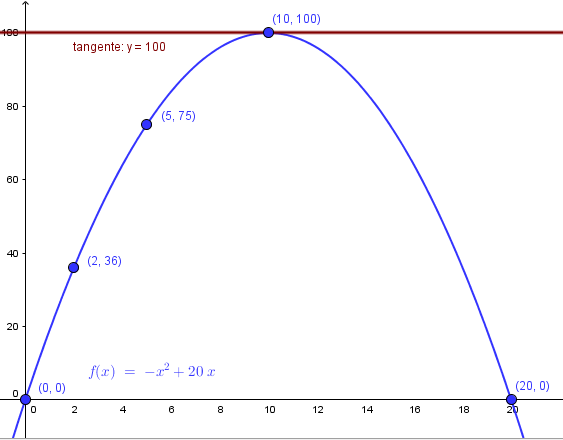
Yo pido que tengáis mucha suerte, porque en vista de que se mantienen año tras otro esos ejercicios de enunciados tan absurdos me parece que no hay allí gente bien preparada y pueden calificar de manera ilógica por antojos. Yo lo he hecho de la única forma en que ese ejercicio tiene algún sentido, después de mis años de estudio y las cerca de 20000 preguntas que llevo respondidas en TodoExpertos.

·

Por cierto, con todo el lío me dejé una pregunta sin contestar en

2b) ¿Cuál es la relación que existe entre el tiempo y el número de tapas que se juntaron y cuál sería el total de tapas en punto máximo en conjunto con lo ya obtenido por la asociación con anterioridad?

La relacíon ya la calculamos

$$\begin{align}&g(x) = -\frac{x^3}{3}+10x^2+60\\&\\&\text{Donde x es el tiempo. Ellos lo llamaron x}\\&\text{en lugar de t que es lo habitual y generaron}\\&\text{confusión con ello, pero yo no lo cambio}\end{align}$$

La pregunta vuelve a ser confusa, en el punto donde más tapas habrá será en el día 20, pues hasta el día 20 todos los días se consugue un número positivo de tapas. por lo tanto el máximo de las tapas obtenidas es

$$\begin{align}&g(20) = -\frac{20^3}{3}+10·20^2+60 =\\&\\& -\frac{8000}{3}+4000+60 =\\&\\&\frac{-8000+ 3·4060}{3}=\frac{4180}{3}=\\&\\&1393.3333...\text{miles de tapas}=\\&\\&1\,393\,333\, tapas\\&\\&\text{Pero se pueden referir a las tapas}\\&\text{que hay cuando se recolectan más}\\&\text{que es el día 10, entonces será}\\&\\&g(10) = -\frac{10^3}{3}+10·10^2+60 =\\&\\& -\frac{1000}{3}+1000+60 =\\&\\&\frac{-1000+ 3·1060}{3}=\frac{2180}{3}=\\&\\&726.66666....\text{ miles de tapas}=\\&\\&726\,667 \;tapas\\&\\&\text{he redondeado al alza, me gustaba más}\\&\\&\\&\\&\end{align}$$

Ya digo que como el enunciado no está claro del todo no sé cuál sería de las dos respuestas, aunaque yo me inclinaría por la segunda.

Y eso es todo.

Saludos.

:

:

No puedo más, estoy viendo el vídeo que me han dado: Video de tutora de la Prepa

Y mi enfado va en aumento. No tienen ni idea. Esta hablando de tres variables, nuemero de tapas, ganancias y tiempo cuando los ejes solo sirven poara dos variables y no sabe en qué eje pone cada una de las variables aparte de que tiene que meter dos en el mismo porque son tres y no tiene la má minima idea de lo que está haciendo.

El enunciado de un problema de esos que yo he hecho cientos es así:

Tenemos una función f(t) que representa el número diario de tapas que se consiguen y tenemos un numero de tapas inicial.

Y ahí podemos calcular por ejemplo cuál es el día que más tapas se consiguen mediante la técnica derivada igualada a 0.

Y la otra pregunta que se puede hacer es cual es el número de tapas acumuladas que se tienen determinado día. Eso se calcula haciendo la integral indefinida y dándole un valor adecuado a la constante de integración par que la función valga la cantidad inicial cuando t=0

Ese es el problema y todo lo que está haciendo en el vídeo está mal. Yo os digo lo que hay que hacer, lo que hace ella no puedo hacerlo porque está mañ y no tiene ningún sentido y los ingenieros que salgan con esa formación que está dando se les caerán los puentes que hagan.

Por lo tanto abandono, esto es superior a mí y a lo que cualquier matemático puede aguantar de alguien que no tiene ni idea de lo que hace.

Saludos.

:

:

Me ha llegado un nuevo vídeo de cómo resolver la tarea: Vídeo del proyecto integrador

Este está algo mejor, tiene algún fallo pero reconoce que en el eje X va el tiempo, algo importante pero no lo es todo.

Bueno, al menos explica como debéis hacer las gráficas, así ya sé lo que os piden y aprendo que llaman recta secante a la derivada, algo que en ningún sitio se llama así, pero por lo menos ya lo sé porque antes no conocía ese significado de recta secante.

Entonces la gráfica que piden es esta:

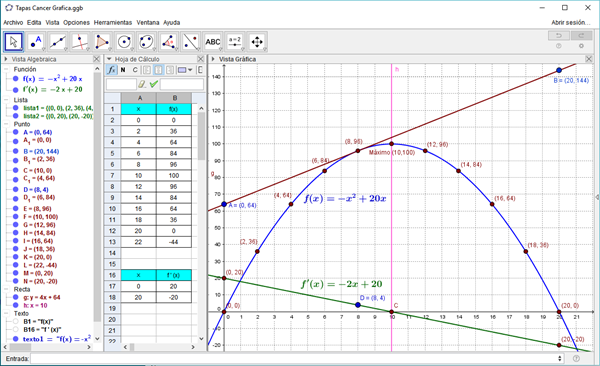
Este es el enlace donde está la gráfica en Geogebra: Gráfica buena Geogebra

Ya sabéis que debéis hacerla a mano pero esto os ayudará. Como veis se ha hecho una tabla de la función para x=0, 2, 4, 6, ..., 22 esos puntos se llevan a la gráfica y se traza la curva que pasa por ellos.

Luego se deriva la función y nos da lo que ellos llaman "recta secante" que es

f'(x)=-2x + 20

Como esa es una recta solo necesitamos dos puntos que tenemos en la segunda tabla y se traza la recta entre esos dos puntos.

Se calcula el máximo trazando la perpendicular al punto donde la recta secante corta al eje X. La secante corta al eje en x=10 y al trazar la perpendicular corta a la función en el punto (10, 100) luego el máximo es 100.

Luego piden trazar la tangente en un punto, yo lo hice en el punto x=8. Vosotros lo tenéis que hacer a mano y luego tenéis que calcular la pendiente de esa tangente, eso se hace tomando dos puntos distantes de la recta, yo tome los puntos:

A(0,64)

B(20, 144)

y la pendiente se calcula como

m= (144-64) / (20-0) = 80/20 = 4

Y ahora vemos que esta pendiente es la misma que el valor de la "recta secante" en x= 8 ya que

f'(8) = -2·8 + 20 = -16 + 20 = 4

Lo mio es para ayudar, debéis ver el vídeo y entender esta parte de hacer la gráfica.

Y la parte donde se calcula las tapas que había en determinado punto la tienen mal porque no explican lo que es la función. La función no indica el número de tapas que hay sino las tapas que se obtienen en cada día, para obtener la número de tapas hay que integrar la función, pero a eso no han llegado todavía los profesores.

Si f fuera el número de tapas, que tienen qué sentido tendría que el día 11 tengan menos tapas que el 10. No es eso, lo que dice la función es que el día 11 recolectan menos tapas que el día 10.

Por eso en lo del apartado 3 me reafirmo en lo que hice.

Escribo sin ver la ampliación que mandé antes por mal funcionamiento de la página, espero que con el tiempo se vean todas. Me equivoqué en decir que no estaba de acuerdo en el apartado 3, donde no estoy de acuerdo es el apartado 2b)

Como ya dije el apartado 2b) se hace como dije muy al principio, mediante integración. Es lo propio que cuando te dan una cantidad inicial es porque se necesita par poder dar un valor concreto a la constante de integración.

La función f(x) no puede ser el número de tapas recolectadas, no puede ser porque si lo fuera sería creciente, cada día habría que tener más, pero aquí lo que pasa es que el día 11 tienes menos tapas recolectadas en total que el día 10, eso es absurdo.

Lo que es la función f(x) y eso entronca con miles de problemas de ecuaciones diferenciales es el número de tapas que se consiguen cada día, ahí si que puede ser decreciente porque unos días se recojan menos tapas que otros.

O sea, la función f(x) es la razón del cambio del número total de tapas, o dicho de una forma más entendible es la derivada de la función tapas totales recolectadas hasta el día x. Así que para obtener las tapas totales recolectadas se tiene que integrar la función f(x) y todos los cálculos son como los hice yo.

Cuando pongan un problema que lo piensen, las funciones no se pueden poner al azar, deben seguir algunas normas para no caer en sucesos absurdos.

Luego si queréis calcular el número de tapas como os dicen en el vídeo hacerlo, pero yo os lo habré enseñado así.

Y respecto el apartado 3c)

Qué relación existe entre el punto máximo alcanzado y la recta secante y su pendiente; relacionarlo con los datos obtenidos en tu actividad.

Una vez que ya he entendido que querían decir con la expresión "recta secante", algo nuevo para mí que yo siempre había llamado a eso derivada, la relación es que cuando la recta secante corta al eje X en un punto (xo, 0) entonces la pendiente de la tangente en el punto (xo, f(xo)) es 0, es decir, la tangente en el punto máximo de la curva es horizontal.

Y eso es todo, saludos.

:

:

Por fin han hecho una corrección del ejercicio en la buena línea, aquí tenéis este vídeo donde el enunciado ya está claro: https://youtu.be/-JPaKgqeOZ8

No obstante no ha terminado de estar bien del todo. Este era un ejercicio inmejorable para introducir las integrales definidas y el cálculo lo ha hecho por sumatorios en lugar de por integrales definidas, eso es lo que me ha defraudado del vídeo.

Algunos pedís como sería con 16000 tapas iniciales en lugar de 60000. Es muy sencillo, la gráfica última, que es la buena, no cambia para nada. Solo cambia la pregunta del número de tapas recolectadas en el punto máximo.

$$\begin{align}&g(x) = \int f(x)dx=\int(-x^2+20x)dt=\\&\\&-\frac{x^3}{3}+10x^2+C\\&\\&\text{Ahora hay que calcular C para que g(0) sea 16 miles}\\&\\&g(0) = C = 16\\&\\&\text{luego la función tapas recogidas hasta el tiempo x es}\\&\\&g(x) = -\frac{x^3}{3}+10x^2+16\\&\end{align}$$

La pregunta vuelve a ser confusa, en el punto donde más tapas habrá será en el día 20, pues hasta el día 20 todos los días se consigue un número positivo de tapas. por lo tanto el máximo de las tapas obtenidas es:

$$\begin{align}&g(20) = -\frac{20^3}{3}+10·20^2+16 =\\&\\& -\frac{8000}{3}+4000+16 =\\&\\&\frac{-8000+ 3·4016}{3}=\frac{4048}{3}=\\&\\&1349.3333...\text{miles de tapas}=\\&\\&1\,349\,333\, tapas\\&\\&\\&\text{Pero se pueden referir a las tapas}\\&\text{que hay cuando se recolectan más}\\&\text{que es el día 10, entonces será}\\&\\&g(10) = -\frac{10^3}{3}+10·10^2+16 =\\&\\& -\frac{1000}{3}+1000+16 =\\&\\&\frac{-1000+ 3·1016}{3}=\frac{2048}{3}=\\&\\&682.66666....\text{ miles de tapas}=\\&\\&682\,667 \;tapas\\&\\&\text{he redondeado al alza, me gustaba más}\\&\\&\\&\\&\end{align}$$

Visto lo que ha hecho algún profesor, es esta segunda la cantidad que habría que poner.