Desarrollo para la resolución de cada punto con sus gráficas correspondientes, para la recta secante y la tangente.
¿Qué producto entregarás?
Un documento, en procesador de textos, donde presentes el desarrollo para la resolución de cada punto con sus gráficas correspondientes, para la recta secante y la tangente.
¿Qué hacer?
Imagina que es posible generar una función que modela para x toneladas de jitomate el costo necesario de su producción f(x). Supongamos que la función que modela el costo por toneladas está dada por:
f(x) = 2x2 + 3x
Recuerda que las funciones son usadas para modelar el comportamiento de algún fenómeno y así poder estimar los valores de la función cuando hay una variación en x.La fórmula para calcular la pendiente de la recta secante a una función dada es:
Ahora resuelve lo que se te pide:
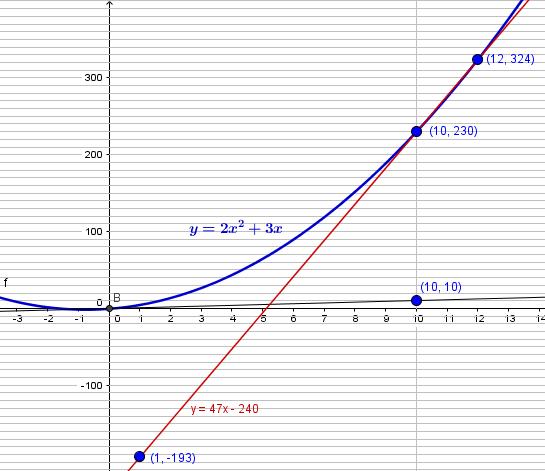
A partir de la fórmula mencionada determina la pendiente (m) de la recta secante para la función de costo de producción de 10 a 12 toneladas.
Para ello, recuerda lo siguiente:
• Utiliza la pendiente m de la recta secante para calcular la razón de cambio promedio del costo de jitomate de 10 a 12 toneladas. Recuerda que X1 será el primer valor de las toneladas y X2 el subsecuente.
• Luego sustituye los valores y obtén la pendiente de la recta secante. La pendiente de la recta secante por dos puntos de la gráfica de la función se interpreta como la razón promedio de cambio del costo por tonelada.
Realiza la gráfica de la recta secante de la función x = 1.
f(x) = 2x2 + 3x
La gráfica de la recta secante con x=1 se debe derivar a partir de la función de costo de producción:
Función de costo de producción
f(x)=2x2 + 3x
Función de costo de producción derivada
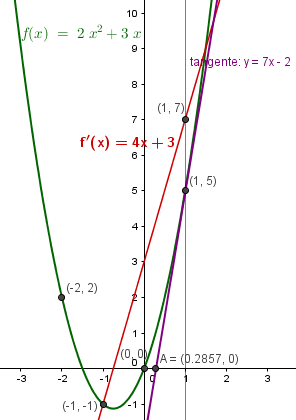
f' (x) = 4x + 3
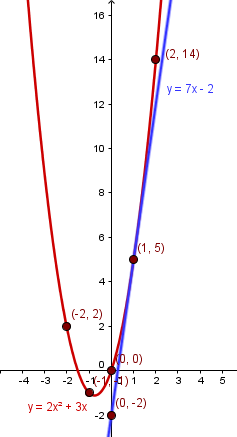
En seguida saca la recta tangente y represéntala en una gráfica.
Recuerda que si quieres obtener y y realizar la gráfica de la recta tangente debes utilizar la función del costo de producción y sustituir el valor de x=1.
Posteriormente utiliza esta fórmula para obtener la tangente despejando y.
y - y1 = m(x - x1)
Al realizar la gráfica emplea una tabla con un rango de x de -2 a 2 y en la gráfica para el eje y un valor máximo de 10 y un mínimo de 2.
http://148.247.220.199/pluginfile.php/10237/mod_assign/intro/grafica.png
Integra tus procesos y gráficas (pueden ser a mano, en Excel o con otro programa especializado) en un solo archivo y súbelo a la plataforma con el siguiente nombre:

profe,podría poner el enlace de la gráfica,para que hagamos pequeños cambios y no se vean todas igual.Gracias - Celia Tejeda
Ya está, ya lo subí Isa. - Valero Angel Serrano Mercadal
muchas gracias usted siempre tan atento - Celia Tejeda
Si profe son dos gráficas. - Anónimo
Muchísimas gracias por todo su apoyo, verdaderamente estoy muy agradecida. A mi en lo particular, no se me da, ni se me dará nunca las matemáticas. Saludos desde México. - lula montiel
Muchísimas gracias,Dios lo bendiga. - Paulina Castillo
Profesor no puedo hacerla modificación de las gráficas, no me abre el archivo - Paulina Castillo
a mi tampoco - Celia Tejeda
Paulina. ¿Pero tienes instalado el programa GeoGebra? Hay que tenerlo para abrir ese fichero. - Valero Angel Serrano Mercadal
Buen día Isa. Yo descargue el archivo y luego lo abrí con geogebra en línea para modificar y luego lo guardé en mi compu. Aprovecho para agradecer al profesor Serrano su valiosísimo apoyo. - federico alejandro campos
Muchas gracias Federico. - Valero Angel Serrano Mercadal
Hola federico, a mi no me salen las gráficas me puedes decir como por favor - Anónimo
Muchas gracias, me ayudó mucho Profesor, ya que yo, hace años no estudio esto. Mil gracias nuevamente. - Gaby Montes
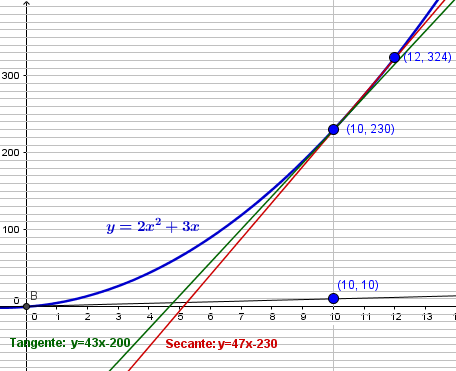
Hay una nueva gráfica en la respuesta, no la piden bien pedida pero yo pienso que podrían querer eso. - Valero Angel Serrano Mercadal
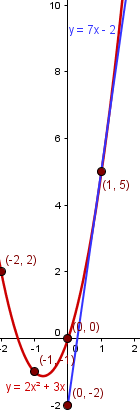
¿Profe en la segunda gráfica esta la secante con azul y la tangente con rojo verdad? ¿Y los datos de la otra ya no se ocupan? - Celia Tejeda
No Isa, la secante es la recta roja, y la función azul es la función de costo de producción. La tangente en x=1 no está en esta, no pedían que salieran las dos juntas, en realidad no sabían lo que pedían. Ahora que lo pienso se podía haber dibujado también la tangente en x=1 pero no se me ocurrió. - Valero Angel Serrano Mercadal
Ah, a lo mejor te confunde una recta fina negra que he hecho que pasa por el punto (10,10). Esa recta no es nada de lo que piden, solo la puse para que os deis cuenta que esa recta sería la diagonal que forma 45º con los ejes, para que veáis que la gráfica está muy distorsionada para que quepa todo y se vea bien. - Valero Angel Serrano Mercadal
Ah, a lo mejor te confunde una recta fina negra que he hecho que pasa por el punto (10,10). Esa recta no es nada de lo que piden, solo la puse para que os deis cuenta que esa recta sería la diagonal que forma 45º con los ejes, para que veáis que la gráfica está muy distorsionada para que quepa todo y se vea bien. - Valero Angel Serrano Mercadal
Buenos días Mtro. Valero. ¿Es posible obtener el fichero de la gráfica de los límites: x en [-2 y 2], y en [-2, 10]" ? - PeAr JeMa
ANONI MO te paso el link de un video https://www.youtube.com/watch?v=In3qLE1E_II ojalá te sirva. - federico alejandro campos
¡Hola Pear! En Geogebra puedes hacer zoom o puedes aumentar o disminuir la ventana de modo que se vea lo que tu quieras. Y con un capturador de pantalla puedes tomar solo el rectángulo que quieras. O puedes guardar la imagen de todo y luego con un programa de dibujo recortas lo que sobra. - Valero Angel Serrano Mercadal
Gracias Mtro. Valero, es justo lo que he hecho. He tomado captura de pantalla y he recortado. Muchas gracias. - PeAr JeMa
Maestro la que nos esta brindando es incalculable mil gracias por su ayuda, consejos y enseñanza, - jose daniel cebreros pardo
Hola esa tal brenda salazar por que usurpa mi nombre? a caso quiere perjudicarme? QUE POCA MAD...! - bonitaa salazar
hola maestro si x=10 en vez de x=1 - Alejandro de la vega
Hola Alejandro. Eso sí que tendría mucho sentido, pues estaríamos comparando la secante que pasa por 10 con la tangente que pasa por 10. Sabemos que la tangente es el limite de la secante cuando la distancia entre los puntos tiende a cero y es educativo ver eso. Pero es que el enunciado dice x=1, yo no lo puedo cambiar, decídselo al profe. - Valero Angel Serrano Mercadal
Lo que pasa es que el dibujo bonito, con la función, la secante ente 10 y 12 y la tangente en 10 no se puede ver en el exiguo rango de x en [-2, 2] y y en [2,10] que dicen, ya ves que necesita uno rangos muy grandes de y distorsionados para que se pueda ver. El ejercicio es absurdo. - Valero Angel Serrano Mercadal
¿Cuántas gráficas son en esta actividad 2 o 1? - Gibi Rock
¡Hola Gibi! Yo no sé cuántas piden, es todo tan confuso e imprevisible que no lo sé, yo he hecho todo lo posible e imposible por entenderlo. - Valero Angel Serrano Mercadal
LISTO ME CALIFICARON CON 100 ... LA PENDIENTE ES : m47 CON EL MISMO DESARROLLO DEL PROFE VALERO.. SECANTE: y=5 y tangente: y=7x-2 con el dearrollo del profe valero, las gráficas utilice las del profe valero, sin ningún problema solo traten que sea al modo y estilo de la prepa ya que yo le di copy paste del profe valero y me dieron un cero, corregí al estilo prepa y ya saque 100 ...animo - Anónimo
Hola @Anoni Mo oye no seas malo ayudame, con esta tarea, en verdad estoy demasiado buey como para entender hasta la respuesta jejejejejejejeje, prometo cambiar todo el formato, ojala se pueda, mi correo es [email protected] en verdad te lo agradeceria enormemente. Saludos - Juan M. Rosales
Anoni mo no seas malo concuerdo con Juan M. Rosales podrás compartir tus actividades a [email protected]. solo tengo hasta hoy - Chacuil cha
No se quieren ni despeinar! Todo esta claro! De todas maneras ya se los envíe por correo tienen que esforzarse ... tantito más y piden nieve de limón. - Anónimo