Calcular la superficie generada al rotar la curva
El siguiente problema plantea:
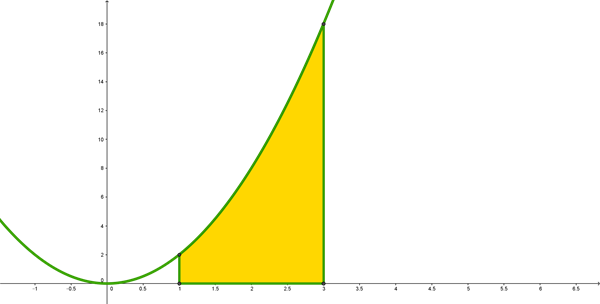
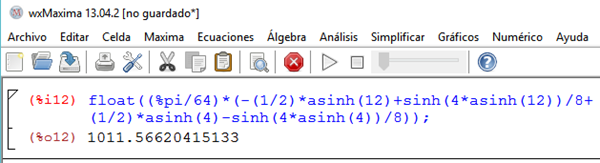
Calcular la superficie generada al rotar la curva la siguiente función
$$\begin{align}&f(x)=2x^2\end{align}$$entre los puntos (1,2) y (3,18)
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1