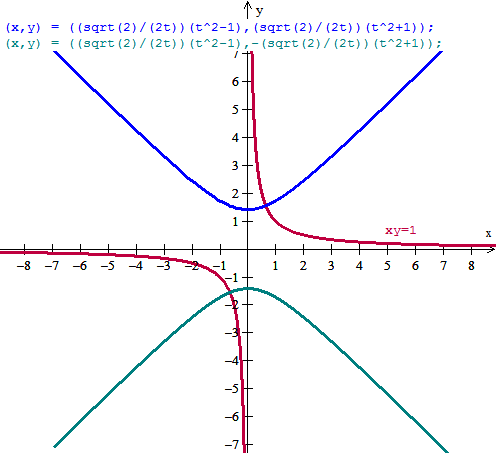
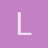1. Halle la ecuación que resulta al girar 45° la ecuación XY=1
- Halle la ecuación que resulta al girar 45° la ecuación XY=1
- Elimine el término xy de la ecuación y grafíquela
- Una persona se encuentra en la cima de una colina y dispara un dardo con una pistola. La trayectoria descrita por el dardo está dada por la ecuación donde t es el tiempo en segundos h (t) es la altura que alcanza el dardo medida en metros, calcule:
- Altura de la colina
- Altura máxima que alcanza el dardo
- Tiempo en que alcanza la altura máxima
- En cuanto tiempo choca contra el piso
- A que distancia horizontal cae el dardo respecto de la persona que lo lanzó
2 Respuestas
Respuesta de albert buscapolos Ing°
2
Respuesta de Valero Angel Serrano Mercadal
2