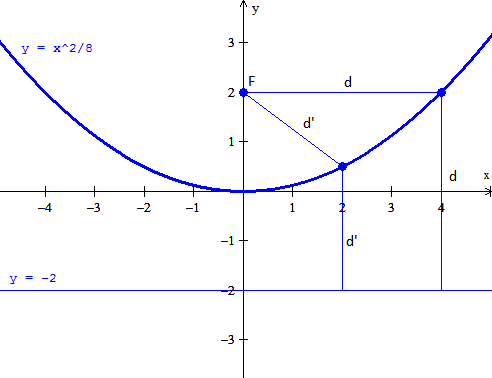Tengo algunas dudas con estos ejercicios de Geometría A.
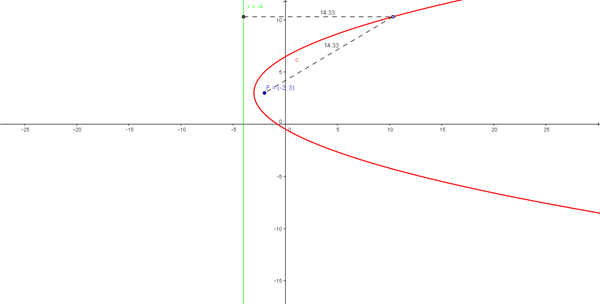
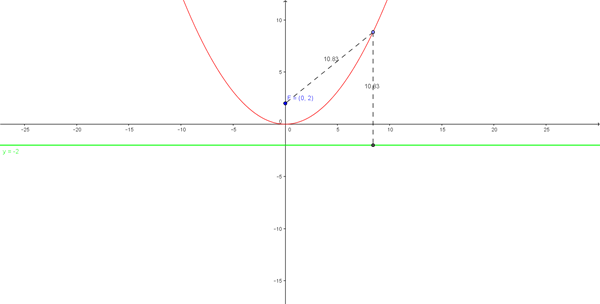
Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta y+2=0 es siempre igual a su distancia del punto A(0,2) Rp. X2=8y
2 respuestas
Respuesta de Lucas m
1
Es la definición geométrica de una parábola donde A es el Foco y Y+2=0 la directriz:
$$\begin{align}&\vec{AP}=P-A=(x,y-2)\\&\\&dist(A,P)=|\vec{AP} |=\sqrt {x^2+(y-2)^2}\\&\\&dist(P,r)=\frac{|y+2|} {\sqrt 1^2}=|y+2|\\&Igualando:\\&\\&\sqrt {x^2+(y-2)^2}= |y+2|\\&Elevando \ al \ cuadrado:\\&x^2+(y-2)^2=(y+2)^2\\&\\&x^2+y^2-4y+4=y^2+4y+4\\&\\&x^2=8y\end{align}$$Adjunto gráfica:
Saludos
:
:
Por error adjunte la gráfica del otro ejercicio.
Es esta:
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Juan!
Por definición eso es una parabola con foco (0,2) y con directriz la recta y=-2
No sé si quieren que la resuelvas por lo de ser una parábola o por igualación de distancias.
Si no sabes teoría de cónicas lo más seguro es hacerlo de la segunda forma.
La distancia de un punto (x, y) a la recta y=-2 es
|y-(2)| = |y+2|
La distancia al punto A(0,2) es
$$\begin{align}&d((x,y),(0,2))=\sqrt{(x-0)^2+(y-2)^2}\\&\\&\text{Las igualamos}\\&\\&|y+2|=\sqrt{x^2+(y-2)^2}\\&\\&\text{elevamos al cuadrado}\\&\\&y^2+4y+4=x^2+y^2-4y+4\\&\\&4y=x^2-4y\\&\\&8y= x^2\\&\\&y = \frac {x^2}{8}\end{align}$$Y la gráfica es esta.
:
: