Determina este problema de optimización
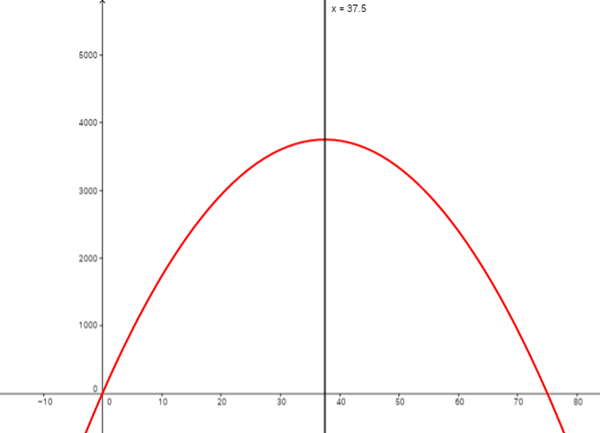
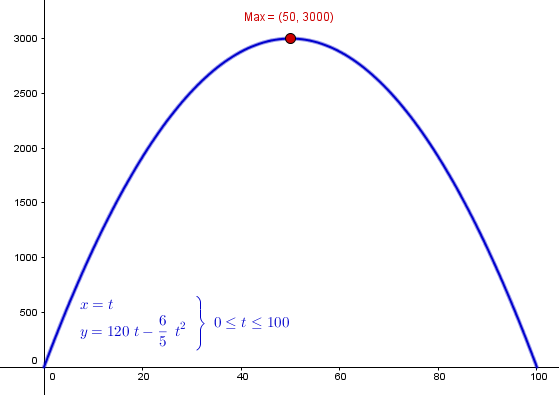
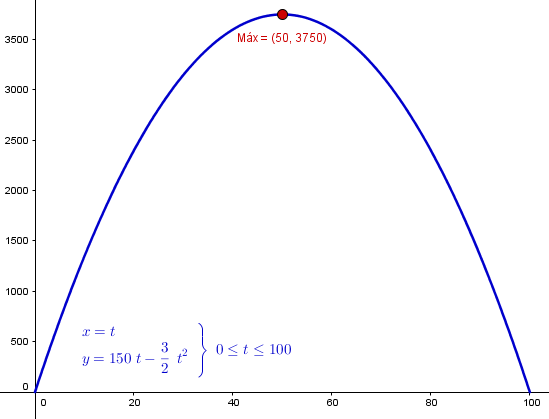
Un hacendado tiene 300 m de malla para cercar dos corrales rectangulares iguales y contiguos, es decir, que comparten un lado de la cerca. Determinar las dimensiones de los corrales para que el área cercada sea máxima. No olvides plantear la función a optimizar (la del área) así como su gráfica.
2 Respuestas
Respuesta
2
Respuesta de Valero Angel Serrano Mercadal
1