Ayuda con rectas y vectores

Haremos un buen dibujo para entenderlo. Es el 80% o más del problema, aparte de saber lo que es la proyección ortogonal y el complemento ortogonal y que entre sí son perpendiculares.

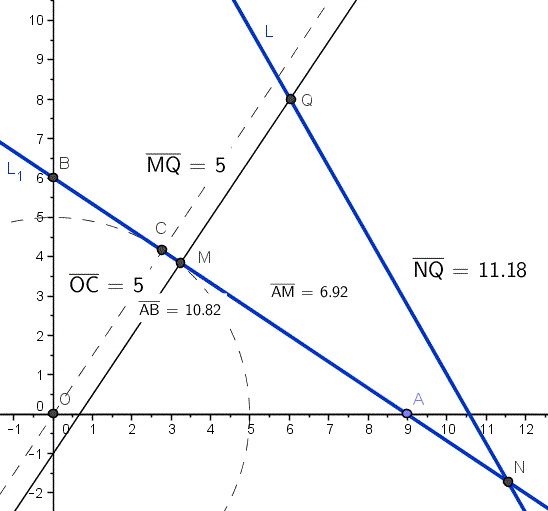
Ese NQ = 11.18 es 5sqrt(5)

El AM = 6.92 son los 16/25 de 10.82 que me dio la distancia AB. Asi se cumple 9AM=16AB, aunque en el problema no nos dan ninguna de esas distancias, solo la proporción.

Por el teorema de Pitágoras podemos calcular NM

NM = sqrt{[5sqrt(5)]^2 - 5^2} = sqrt (125-25) = sqrt(100) = 10

Y podemos calcular AB = sqrt(A^2 + B^2)

Y el punto M por proporción de triángulos es ( (9/25)A, (16/25)B)

Luego el punto N situado a distancia 10 será en la recta AB será:

L1: (9A/25, 16B/25) + t(A, -B)

N = (9A/25, 16B/25) + [10/sqrt(A^2+B^2)](A, -B)

Ahora vamos a calcular el punto Q, lo haremos sumando al punto M el vector perpendicular a la recta L de longitud 5

Q = (9A/25, 16B/25) + [5/sqrt(A^2+B^2)](B, A)

Y conocidos N y Q conocemos la recta en forma paramétrica

L: Q + t·QN

QN es el vector de Q a N que es

(9A/25, 16B/25) + [10/sqrt(A^2+B^2)](A, -B) - (9A/25, 16B/25) - [5/sqrt(A^2+B^2](B, A) =

[10/sqrt(A^2+B^2)] (A-2B, -B-2A)

L: (9A/25, 16B/25) + [5/sqrt(A^2+B^2)](B, A) + [10/sqrt(A^2+B^2)]t(A-2B, -B-2A)

Me he liado de qué manera. No sabes de que manera.

Se me olvidó que la recta pasaba por (1,7) y que la pendiente era positiva.

Pero no puedo dejar todo esto que he hecho, me ha llevado horas. Por favor, puntúalo y vuélveme a mandar la pregunta.