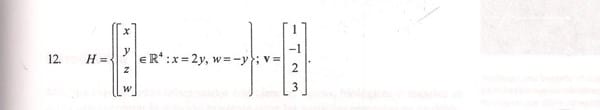Bases ortonormales, proyecciones ortogonales.

Me guiaré por lo que he encontrado en esta página.

Proyección ortogonal

a) Lo primero debemos encontrar una base del espacio H

H = {(x, y, z, t) € R4 | x=2y, w = -y}

La coordenada z no tiene ninguna ligadura, puede tomar cualquier valor.

Daremos cualquier valor a w y a partir de él calculamos los valores para x e y

y = -w

x = 2y = -2w

La forma de los vectores del espacio H será

(-2w, -w, z, w)

Que se puede poner como combinación lineal de estos dos

u1=(-2, -1, 0, 1)

u2=(0, 0, 1, 0)

Y es un problema fácil porque los vectores de la base son ortogonales, ya que su producto escalar es claramente cero.

Las coordenadas respecto de esta base de la proyección ortogonal de un vector v son los productos escalares de los elementos de la base por v y divididos por la norma de los vectores de la base.

$$p(v)=\frac{\lt v,u_1\gt}{||u_1||^2}u_1+\frac{\lt v,u_2\gt}{||u_2||^2}u_2\\ \\ \\ \text{El vector v es (1,-1,2,3)}\\ \\ ||u_1||^2=(-2)^2+(-1)^2 +0^2+1^2 =6\\ \\ ||u_2||^2=1^2 = 1\\ \\ \lt(1,-1,2,3),(-2,-1,0,1)\gt=-2+1+0+3=2\\ \\ \lt(1,-1,2,3),(0,0,1,0)\gt=2\\ \\ p(v)=\frac{2}{6}(-2,-1,0,1)+\frac{2}{1}(0,0,1,0)=\\ \\ \left(-\frac 23,-\frac 13,0,\frac 13\right)+(0,0,2,0)=\left(-\frac 23,-\frac 13,2,\frac 13\right)$$

b) El espacio ortogonal a H es el formado por los vectores ortogonales a todos los vectores de H, es decir aquellos cuyo producto escalar es cero.

H = {a(-2, -1, 0, 1) + b(0, 0, 1, 0) | a,b € R}

Un vector de h será

h = (-2a, -a, b, a)

y uno (x,y,z,t) ortogonal cumplirá

-2ax -ay + bz +at = 0 para todo a,b€R

a(-2x-y+t) + bz = 0

Y para que esto se cumpla para cualquier a, b se debe cumplir

-2x-y+t = 0

z=0

Tomando y, t como parámetros tendremos

-2x = y-t

x = (y-t)/(-2) = t/2-y/2

y la forma del vector será

( t/2-y/2, y, 0, t)

o para quitar los denominadores

(t-y, 2y, 0, 2t) = (t, 0, 0, 2t) + (-y, 2y, 0,0) = t(1, 0, 0, 2) + y(-1, 2, 0, 0)

Tenemos la base B={(1, 0, 0, 2), (-1, 2, 0, 0)} para el espacio ortogonal de H

Lamentablemente esa base no es ortogonal ya que el producto escalar de los dos vectores es -1

Hay que ortogonalizarla por el método de Gram-Schmidt

Tomaremos el primer elemento de la base como elemento de la base ortogonal

u1 = (1, 0, 0, 2)

Y como segundo elemento de la base ortogonal tomaremos el segundo de la la base menos la proyección del segundo de la base sobre el primero de la ortogonal.

$$u_2=b_2-proy_{u_1}(b_2)\\ \\ u_2=b_2-\frac{\lt u_1,b_2\gt}{\lt u_1,u_1 \gt}u_1\\ \\ \\ u_2=(-1, 2, 0, 0)-\frac{-1}{5}(1,0,0,2)=\\ \\ u_2=\left(-\frac 45,2,0,\frac 25\right)\\ \\ \text {La norma del segundo vector es:}\\ \\ \\ \sqrt{\frac{16}{25}+4+\frac{4}{25}}= \sqrt{\frac{120}{25}}=\frac{2 \sqrt {30}}{5}\\ \\ \\ \text{y la base ortonormal es:}\\ \\ \\ B=\left\{\left( \frac{1}{\sqrt 5},0,0,\frac{2}{\sqrt 5}\right),\left(\frac{-2}{\sqrt {30}},\frac{5}{\sqrt{30}},0,\frac{1}{\sqrt{30}} \right) \right\}$$

c) v = p+q con p € H y q € ortogonal(H)

Ya calculamos la proyección ortogonal al principio, luego ese será el elemento p de H y el del ortogonal será el vector que falta para que se cumpla la identidad

(1, -1, 2, 3) = (-2/3, -1/3, 2, 1/3) + q

q=(1+2/3, -1+1/3, 2-2, 3-1/3) = (5/3, -2/3, 0, 8/3)

Luego

p=(-2/3, -1/3, 2, 1/3)

q=(5/3, -2/3, 0, 8/3)

Y eso es todo, epero que te sirva y lo hayas entendido.