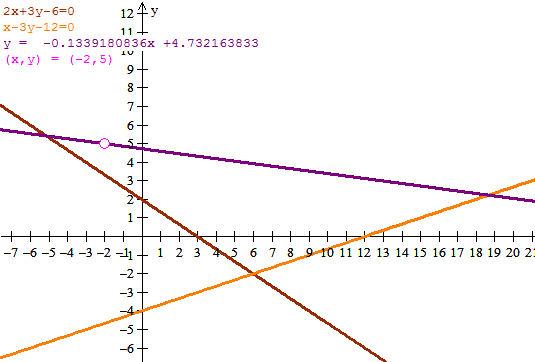Necesito ayuda con una ecuación de la recta

Es necesario hacer la gráfica ya que las dos rectas determinan cuatro triángulos y solo uno de ellos sirve. Y analíticamente es difícil saber cuál y aun más difícil explicarlo.

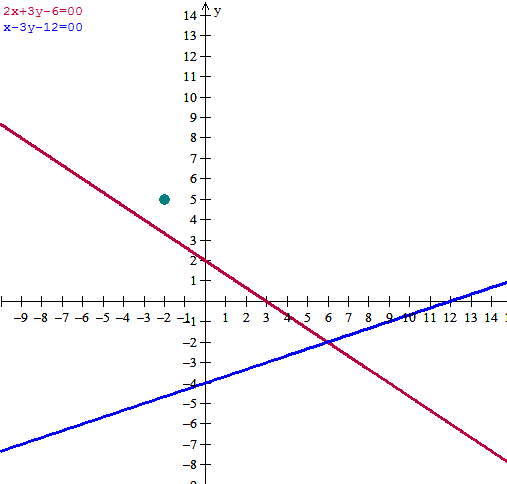
La intersección la calculamos resolviendo las ecuaciones
2x + 3y - 6 = 0
x - 3y - 12 = 0
Sumándolas
3x -18= 0
3x = 18
x=6
2·6 + 3y - 6 = 0
3y + 6 = 0
y = -2
Luego es el punto (6, -2)
El vector director de una recta Ax+By+C= 0 es (B,-A) o (-B,A)
luego el vector director de L1 es (3, -2) o (-3, 2)

[Atención, en la otra pregunta me confundí al poner (3. -2) o (-2, 3)]

Viendo el dibujo el lado se obtiene a partir del vértice aplicando el vector (-3,2)

[y a partir de aquí las cuentas son distintas porque yo puse (-2,3)]

Y el vector director de L2 es (-3, -1) o (3,1)
Vemos que para formar el lado del triangulo debemos usar el vector (3,1) a partir de la intersección.
Ahora debemos hacer que los dos vectores tengan la misma longitud
El módulo de (-3,2) es sqrt(4+9) = sqrt(13)
El módulo de (3,1) es sqrt(9+1) = sqrt(10)
multiplicaremos (-3,2) por sqrt(10) y (3,1) por sqrt(13) para que tengan el mismo módulo
(-3sqrt(10), 2sqrt(10))
(3sqrt(13), sqrt(13))
Estos dos vectores multiplicados por la misma constante y sumados al vértice nos dan los otros dos vértices

$$\begin{align}&V_2= (6-3k \sqrt{10},\; -2+2k \sqrt{10})\\ &V_3= (6+3k \sqrt{13},\; -2+k \sqrt{13})\end{align}$$

El lado será la recta L3 que los une

$$\begin{align}&L_3: \frac{x - 6 + 3k \sqrt{10}}{6+3k \sqrt{13}- 6+3k \sqrt{10}} =\frac{y + 2 - 2k \sqrt{10}}{-2+k \sqrt{13} +2-2k \sqrt{10}}\\ &\\ &\\ &\\ &L_3: \frac{x - 6 + 3k \sqrt{10}}{3k \sqrt{13}+3k \sqrt{10}} =\frac{y + 2 - 2k \sqrt{10}}{k \sqrt{13}-2k \sqrt{10}}\\ &\\ &\\ &\\ &\text{Simplificamos k en los denominadores}\\ &\\ &L_3: \frac{x - 6 + 3k \sqrt{10}}{3 \sqrt{13}+3 \sqrt{10}} =\frac{y + 2 - 2k \sqrt{10}}{ \sqrt{13}-2 \sqrt{10}}\end{align}$$

sustituimos (x,y) por (-2,5) que es el punto por donde debe pasar

$$\frac{-8 + 3k \sqrt{10}}{3 \sqrt{13}+3 \sqrt{10}} =\frac{7 - 2k \sqrt{10}}{ \sqrt{13}-2 \sqrt{10}}$$

$$\begin{align}&(-8 + 3k \sqrt{10})(\sqrt{13}-2 \sqrt{10})=(7 - 2k \sqrt{10})(3 \sqrt{13}+3 \sqrt{10})\\ &\\ &\\ &\\ &-8 \sqrt{13}+16 \sqrt{10}+3k \sqrt{10}(\sqrt{13}-2 \sqrt{10})=\\ &21 \sqrt{13}+21 \sqrt{10}-2k \sqrt{10}(3 \sqrt{13}+3 \sqrt{10})\\ &\\ &\\ &-8 \sqrt{13}+16 \sqrt{10}+3k(\sqrt{130}-20)=\\ &21 \sqrt{13}+21 \sqrt{10}-2k(3 \sqrt{130}+30)\\ &\\ &\\ &3k(\sqrt{130}-20)+2k(3 \sqrt{130}+30)=\\ &21 \sqrt{13}+21 \sqrt{10}+8 \sqrt{13}-16 \sqrt{10}\\ &\\ &k(3 \sqrt{130}-60+6 \sqrt{130}+60)=29 \sqrt{13}+5 \sqrt{10}\\ &\\ &k(9 \sqrt{130})=29 \sqrt{13}+5 \sqrt{10}\\ &\\ &\\ &k=\frac{29 \sqrt{13}+5 \sqrt{10}}{9 \sqrt {130}}=\\ &\\ &\\ &\frac{(29 \sqrt{13}+5 \sqrt{10})\sqrt{130}}{9 \sqrt {130}\sqrt{130}}=\\ &\\ &\\ &\frac{377 \sqrt{10}+50 \sqrt{13}}{1170}\end{align}$$

Y ahora llevamos este valor a L3

$$\begin{align}&L_3: \frac{x - 6 + 3 \frac{377 \sqrt{10}+50 \sqrt{13}}{1170} \sqrt{10}}{3 \sqrt{13}+3 \sqrt{10}} =\frac{y + 2 - 2 \frac{377 \sqrt{10}+50 \sqrt{13}}{1170} \sqrt{10}}{ \sqrt{13}-2 \sqrt{10}}\\ &\\ &\\ &L_3: \frac{x - 6 + 3 \frac{3770+50 \sqrt{130}}{1170}}{3 \sqrt{13}+3 \sqrt{10}} =\frac{y + 2 - 2 \frac{3770+50 \sqrt{130}}{1170}}{ \sqrt{13}-2 \sqrt{10}}\\ &\\ &\\ &L_3: \frac{x - 6 + \frac {87}{9} +\frac{5 \sqrt{130}}{39}}{3 \sqrt{13}+3 \sqrt{10}} =\frac{y + 2 - \frac{58}{9}-\frac{10 \sqrt{130}}{117}}{ \sqrt{13}-2 \sqrt{10}}\end{align}$$

Y como puedes ver las operaciones para dejarla en la forma y=ax+b van a ser muy complicadas.

Asi que aunque no sea muy ortodoxo voy a sustituir las expresiones por números decimales y así podremos comprobar si esta bien. Simplificando la expresión de L3 queda de esta forma

(x + r) / s = (y + u) / v

r = 5.128430032

s = 20.30348681

u = -5.418953355

v = -2.719004045

la ecuación de la recta queda así

(v/s)(x+r) = y+u

y = (v/s)(x+r) - u

y = -0.1339180836(x+5.128430032) + 5.418953355

y = -0.1339180836x +4.732163833

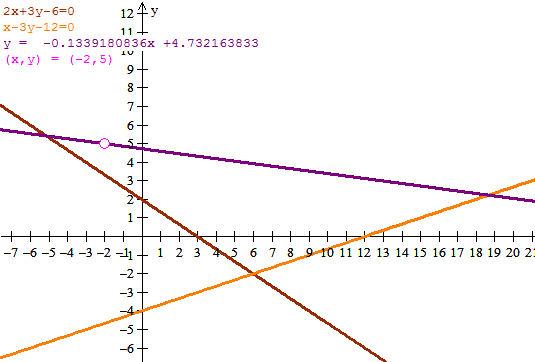
Y por lo que parece está bien.

Ahora que veo el dibujo, creo que habría otra forma más fácil de hacerlo como la recta paralela a la bisectriz que pasa por (-2,5).

Pero ya he trabajado muchísimo con este problema, que hasta que di con la respuesta me equivoqué un par de veces en las cuentas. Puntúa esta pregunta y lo otra que respondí antes y si quieres mándame una nueva en la que usaré ese otro método.