Eliminar el término xy de la curva
Ejercicios de transformación de coordenadas por rotación
1. Por una rotación de coordenadas, elimina el término xy de la curva
$$2x^2+\sqrt{3}xy+y^2$$traza su lugar geométrico y ambos sistemas de ejes coordenados. (Sugerencia: ¿Sustituye las ecuaciones de rotación y resuelve para el ángulo? De tal forma que el coeficiente del término xy se vuelva cero).
Nota: por error le envié otra, ésta es la que me pidió la volviera a enviar.
1 respuesta
Si es que no me aclaro con la matriz de rotación y la de cambio de ejes siempre las confundo.
La de rotación es
Cosa -sina
Sina cosa
Y da las nuevas coordenadas del punto girado con los mismos ejes.
La de cambio de ejes es
Cosa sina
-Sina cosa
Y da las coordenadas nuevas del mismo punto con los ejes girados ese ángulo.
Y de la anterior se duduce que la matriz que dadas las coordenadas tras el giro nos da las viejas es
Cosa -sina
Sina cosa
Esta es la que hay que usar y la que usé la otra vez pero sin convencimiento.
Lo mejor será empezar con la gráfica y así se entiende mejor y se puede comprobar la respuesta al final . Anadí un = 9 a la ecuación para que la curva fuese curva de verdad.
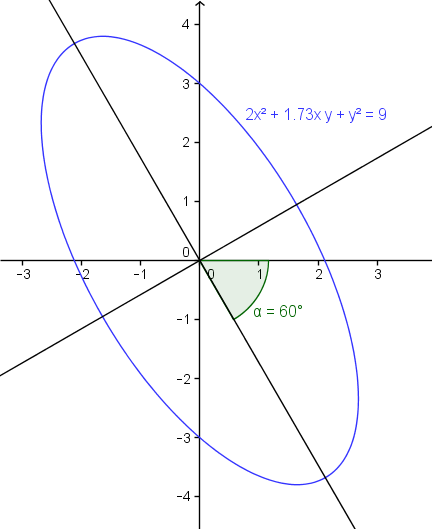
Entonces la ecuación es:
x = zcosa - tsena
y = zsena + tcosa
2x^2 + sqrt(3)xy + y^2 = 9
2(z·cosa - t·sena)^2 + sqrt(3)(z·cosa - t·sena)(z·sena + t·cosa) + (z·sena + t·cosa)^2 =9
2[z^2·cos^2a + t^2·sen^2(a) - 2zt·cosa·sena] +
sqrt(3)[z^2·cosa·sena + zt·cos^2(a) - tz·sen^2(a) - t^2sena·cosa) +
z^2·sen^2(a) + t^2·cos^2(a) + 2zt·sena·cosa = 9
Solo nos interesa dejar a cero la suma de términos que contienen zt
-4cosa·sena + sqrt(3)·[cos^2(a)-sen^2(a)] + 2sena·cosa=
Y aquí me equivoqué en el signo de 2senacosa que debía ser negativo
-2sena·cosa + sqrt(3)·[cos^2(a)-sen^2(a)] =
-sen(2a) + sqrt(3)·cos(2a) = 0
-sqrt[1 - cos^2(2a) + sqrt(3)cos(2a)=0
-sqrt[1 - cos^2(2a)] = - sqrt(3)cos(2a)
Elevamos al cuadrado
1 - cos^2(2a) = 3cos^2(2a)
4cos^2(2a) =1
cos^2(2a) = 1/4
cos(2a) = +- 1/2
2a = pi/3, 2pi/3, 4pi/3, 5pi/3, 7pi/3, 8pi/3, 10pi/3, 11pi/3
a = pi/6, pi/3, 2pi/3, 5pi/6, 7pi/6, 4pi/3, 5pi/3, 11pi/6
Pero puede que alguna no sirva porque al elevar al cuadrado se introducen
soluciones fantasma.
Lo comprobamos con la ecuación corregida
-sen(2a) + sqrt(3)·cos(2a) = 0
-sen(pi/3) + sqrt(3)·cos(pi/3) = -sen60º + sqrt(3)cos60º = -sqrt(3)/2 + sqrt(3)(1/2) = 0
-sen(2pi/3) + sqrt(3)cos(2pi/3) = -sen120º+ sqrt(3)cos120º = -sqrt(3)/2 - sqrt(3)(1/2)
-sen(4pi/3) + sqrt(3)cos(2pi/3) = -sen240º+ sqrt(3)cos240º = sqrt(3)/2 - sqrt(3)(1/2) = 0
-sen(5pi/3) + sqrt(3)·cos(5pi/3) = -sen300º + sqrt(3)cos300º = sqrt(3)/2 +sqrt(3)·(1/2)
...
Siguiendo se comprueba que valen 8pi/3 y 11pi/3
Luego los ángulos validos son 2a=pi/3, 4pi/3, 7pi/3 y 10pi/3
a=pi/6, 2pi/3, 7pi/6 y 5pi/3 = 30º, 120º, 210º y 300º
Y esas son las rotaciones de ejes que hacen que la curva pierda el término en xy. El que pinte en la figura no fue el más afortunado, en realidad el giro sería de esa figura sería -60º que se corresponde con el 300º de las respuestas.
Y eso es todo.
