Ayuda con la hipérbola 2

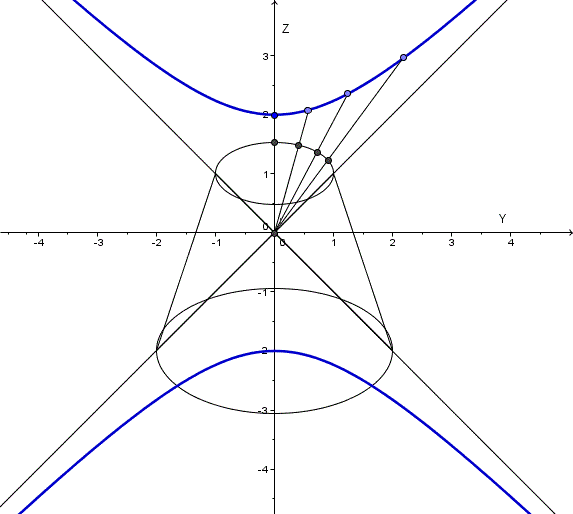
Te ponía al final el caso práctico de las dos grúas que suben un objeto. Ahí también salía una hipérbola.

Pondremos la bombilla en el punto (0,0,0)

La circunferencia superior que tendrá por ecuación

y=a

x^2+y^2= r^2

Donde a es la altura respecto a (0,0,0) del plano que contiene esa circunferencia y r es el radio de arriba

La inferior será

y = b con b negativo

x^2+y^2 = R^2 con R>r

Supongamos que miramos de frente al eje Y y el X viene hacia nosotros

El plano de la pared sera x=c con c negativo

Los rayos de la bombilla que rozan la circunferencia de arriba son rectas que pasan por (0,0,0) y (-sqrt(r^2-t^2), t, a) para t entre -r y r

La recta es

x/-sqrt(r^2-t^2) = y/t = z/a

Para hallar la intersección con la pared extraemos dos planos de la ecuación de la recta

1) tx = - y·sqrt(r^2-t^2)

2) ay=tz

3) x=c

Sustituyendo la x de la 3ª en la 1ª

tc = -y·sqrt(r^2-t^2)

y = -tc/sqrt(r^2-t^2)

Sustituyendo la y recién calculada en la

-atc/sqrt(r^2-t^2) = tz

z = -ac/sqrt(r^2-t^2)

La hipérbola del plano de la pared tiene jos ejes Y y Z y el eje longitudinal es el Z.

Se supone que con dos constantes adecuadas tendremos la ecuación canónica

$$\begin{align}&\frac{z^2}{k^2}-\frac{y^2}{j^2}= 1\\ &\\ &\frac {a^2c^2}{k^2(r^2-t^2)} - \frac{t^2c^2}{j^2(r^2-t^2)}=1\\ &\\ &\frac{a^2c^2j^2-t^2c^2k^2}{k^2j^2(r^2-t^2)} = 1\\ &\\ &a^2c^2j^2-t^2c^2k^2 =k^2j^2r^2-t^2k^2j^2\\ &\\ &\text {la igualdad término a término del polinomio en t}\\ &\texr{es en el término independiente}\\ &\\ &a^2c^2j^2 = k^2j^2r^2 \implies \\ &a^2c^2=k^2r^2\implies \\ &k^2=\frac{a^2c^2}{r^2}\\ &\\ &\text{y en el término con t es:}\\ &c^2k^2=k^2j^2 \implies j^2 =c^2\\ &\\ &\end{align}$$

Y la ecuación de la hipérbola es:

$$\begin{align}&\frac{z^2}{k^2}-\frac{y^2}{j^2}= 1\\ &\\ &\frac{r^2z^2}{a^2c^2}-\frac{y^2}{c^2}= 1\end{align}$$

Puede comprobarse que es verdad sustituyendo en ella los valores de z e y

$$\begin{align}&\frac{r^2}{a^2c^2}\frac{a^2c^2}{r^2-t^2}- \frac{t^2c^2}{c^2(r^2-t^2)}=\\ &\\ &\frac{r^2}{r^2-t^2}-\frac{t^2}{r^2-t^2}= \frac{r^2-t^2}{r^2-t^2}=1\end{align}$$

Luego es verdad que es una hipérbola. En el dibujo queda muy bonita con las dos ramas de la hipérbola, pero eso no será cierto salvo que la bombilla esté muy bien puesta en el punto justo, si no dará dos hipérbolas distintas. Sería mejor un cilindro y la bombilla justo en el centro para obtener las dos ramas de la misma hipérbola.

Y eso es todo.

gracias vale , pero si me pudieras poner el gráfico , esto es lo ultimo que le pido