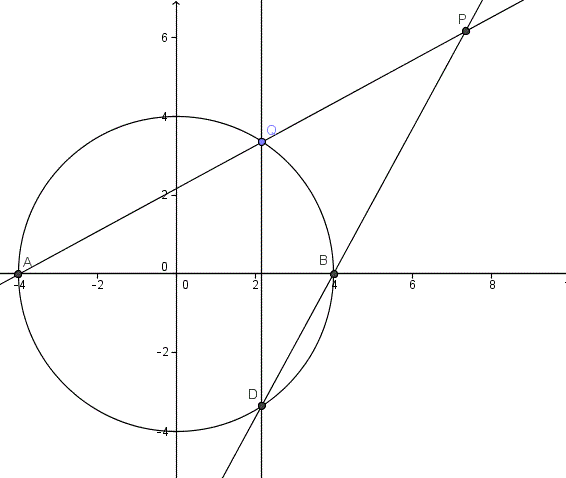Hallar el lugar geometrico
hola vale , si me puedes ayudar:
Dada la circunferencia C: x^2+y^2=16 , desde el extremo izquierdo A , de C , se traza una cuerda variable AQ y desde el extremo superior Q de dicha cuerda se traza una perpendicular al diámetro horizontal AB la cual corta a la curva en el punto D. Se traza la recta DB , la cual se prolonga hasta interceptar en P a la prolongación de la cuerda AQ , halle la ecuación del lugar geométrico de P
1 Respuesta
Habría que saber que tipo de geometría estas estudiando. Si es proyectiva hay un valor que se llama potencia de un punto respecto de una circunferencia y cuyo valor es el producto de las distancias a los dos cortes con la circunferencia de una recta que pase por el punto. Y es un valor igual para cualquier recta que se considere que corte a la circunferencia.
Entonces en el dibujo tendremos
Potencia de P sobre C = PA·PQ = PB·PD
El punto A es (-4,0)
Los puntos de la circunferencia por arriba son
(x, sqrt(16-x^2))
Y por abajo
(x, -sqrt(16-x^2))
La recta AQ será
(-4, 0) + t(x+4, sqrt(16-x^2))
o
(-4, 0) + t(x+4,-sqrt(16-x^2))
Para t=0 tenemos el punto A, para t=1 tenemos el punto Q.
La potencia de un punto de parámetro t de esta recta respecto de la circunferencia será
PQ·PA = (t-1)t·sqrt((x+4)^2+16-x^2) = t(t-1)sqrt(8x+32)
Y esa potencia debe ser la misma que calculada mediante la recta DB
Lo dejo por el momento. Es más complicado de lo que parece. Pero por si te sirve a mi me da la impresión que la figura es la hoja derecha de una hipérbola con vértice en (4,0) estoy casi seguro.
debe salir x^2-y^2=16
Pues lo q
Vaya, se mandó sola la respuesta. No quería mandarle todavía. Pues es precisamente lo que te decía, esa es la ecuación de una hipérbola con centro en (0,0) y el vértice derecho en (4,0).
Espera que lo demuestre, creo que lo potencia de un punto respecto a una circunferencia no ayuda sino que entorpece y voy a probar por ecuaciones de rectas.
Me ayudaría bastante si me dijeras el tema que estas estudiando para saber cuál debe ser el método de resolución.
si vale , mejor hazlo por rectas , pues jamas he escuchado eso de potencia de un punto , en el libro las soluciones de esos problemas lo hacen por rectas
Es una cosa de la geometría proyectiva. Lo vimos en primero de carrera. Aquí lo tienes:
Potencia de un punto respecto de una circunferencia.
Ahora mismo no me puedo poner con el problema, lo intentaré luego.
Habíamos llegado a que la recta AQ era
r1: (-4, 0) + t(x+4, sqrt(16-x^2)) =
Siendo el punto Q (x, sqrt(16-x^2))
El punto D es el simétrico respecto del eje X de Q
D = (x, - sqrt(16-x^2))
Ahora vamos a calcular la recta DB
B=(4,0)
vector BD =(x-4, -sqrt(16-x^2))
Con lo cual la recta BD es
r2:(4,0) + s (x-4, -sqrt(16-x^2))
Vamos a hallar la intersección de las dos rectas igualando las coordenadas
-4 +t(x+4) = 4 +s(x-4)
t·sqrt(16-x^2) = -s·sqrt(16-x^2) ==> t = -s
con ese valor vamos a la primera
-4 -s(x+4) = 4 +s(x-4)
-4 -sx - 4s = 4 +sx -4s
-4-sx = 4+sx
- 8 = 2sx
s = -4/x
El punto de intersección será
P=(4+(-4/x)(x-4), (4/x)sqrt(16-x^2)) =
(4-4+16/x, (4/x)sqrt(16-x^2)) =
(16/x, (4/x)sqrt(16-x^2))
Lo adecuamos
(16/x, sqrt[16(16-x^2)/x^2]) =
(16/x, sqrt[(16/x)^2 -16])
Lo que pasa es que hemos usado la x en referencia a la coordenada x del punto Q. Ahora llamemos x a la coordenada x del punto P para tener la ecuación del lugar geométrico, es hacer el cambio de variable x =16/x
(x, sqrt(x^2-16))
En ecuación es
y=sqrt(x^2-16)
y elevando al cuadrado
y^2 = x^2-16
x^2 - y^2 = 16
Y eso es todo.
