Operaciones con sucesiones y gráficas
Considera la sucesión de funciones {fn(x)} dada por :
fn(x) = (x elevada a la 2n) / (1 + x elevada a la 2n)
Si fn esta definida sobre los reales:
traza la gráfica de las primeras 5 funciones de la sucesión: f1, f2, f3, f4, f5
(sobre un intervalo con centro en 0 y, un radio de al menos 3 unidades. Usando Geogebra.
Determina la regla de correspondencia de la función f a la que la sucesión converge puntualmente en R.
¿La convergencia es uniforme? Justifica tu respuesta.
Y si fn esta definida solo sobre el intervalo [2, 3] demuestra que la convergencia es uniforme y calcula:
lim n--->oo integral definida de 2 a 3 de la función fn(x)dx
1 respuesta
Esta es la gráfica:
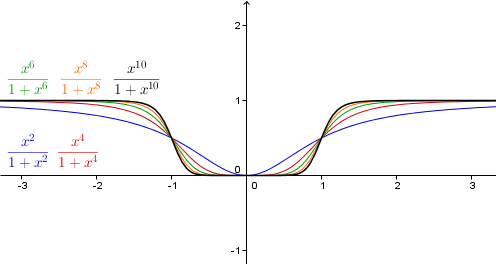
La función a la que converge es
f(x) = 0 si |x| <1
1/2 si x=1
1 si |x|>1
esos son los límites de las sucesiones x^(2n) / [1+x^(2n)] cuando n tiende a infinito según el valor que tenga x
si |x|<1 el límite queda 0/(1+0) = 0
Si |x|=1 obviamente es 1/(1+1)=1/2
Si |x|>1 quedan dos infinitos iguales en numerador y denominador y el límite es 1. Si no te sirve ese argumento utilizas l'Hôpital y la derivada es la misma y el límite es 1.
No hay convergencia uniforme. Para cualquier fn siempre hay un punto x<1 tal que fn(x) =1/4 y si tomamos epsilon=1/8 en ese punto x se cumplirá
|fn(x) - f| = |1/4-0| = 1/4 >1/8 = epsilon
Luego no hay un N que sirva para todos los puntos x a la vez.
En el intervalo 2,3 si que hay convergencia uniforme. Dado el epsilon tomaremos el N tal que
1-FN(x) <epsilon y toda función fn con n >N estará a distancia menos que epsilón de la función
f.
$$\begin{align}&\left|1-\frac{2^{2N}}{1+2^{2N}}\right|\lt \epsilon\\ &\\ &\\ &\left|\frac{1}{1+2^{2N}}\right|\lt \epsilon\\ &\\ &\\ &\frac{1}{1+2^{2N}}\lt \epsilon\\ &\\ &\\ &Si \quad n\gt N\\\ &\\ &\frac{1}{1+2^{2n}}\lt \frac{1}{1+2^{2N}}\lt \epsilon\\ &\\ &\\ &Y\;si\;x\gt 2\\ &\\ &\frac{1}{1+x^{2n}}\lt \frac{1}{1+2^{2n}}<\epsilon\\ &\\ &\\ &luego\\ &\\ &\left|f_n(x)-f(x) \right|<\epsilon\quad \forall n\gt N,\;x \in[2,3]\\ &\\ &\\ &\\ &\\ &\\ &\end{align}$$Y la integral será
$$\lim_{n\to \infty}\int_2^3 \frac{x^{2n}}{1+x^{2n}}dx$$Que va, esa integral no se puede hacer, menuda integral es.
Usaremos un teormea que dice: Sea fn(x) una sucesión de funciones definida en un intervalo A que converge uniforememente en ese intervalo a f(x). Si fn(x) es integrable Riemann para todo n en [a,b] incluido en A entonces f(x) es integrable Riemann en [a,b] y se cumple
$$\begin{align}&\lim_{n \to \infty} \int_a^b f_n(x)dx=\int_a^b f(x)dx\\ &\\ &luego\\ &\\ &\lim_{n \to \infty} \int_2^3 \frac{x^{2n}}{x^{2n}+1}dx=\int_2^31·dx=x|_2^3=1\end{align}$$Y eso es todo.
