Se tienen 2 circunferencias ortogonales los radios miden R y r.la longitud de la tangente común es:

Haremos un dibujo para entenderlo bien.

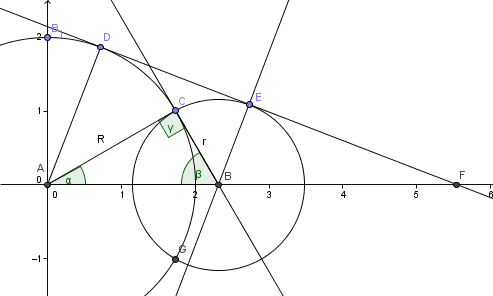
Podemos calcular la distancia AB por el teorema de Pitágoras

AB = sqrt(R^2+r^2)

Los segmentos AD y BE son paralelos porque son ambos perpendiculares a la tangente DF

Entonces los triángulos ADF y BEF son semejantes por tener un ángulo común y lados opuestos paralelos.

Luego los lados son proporcionales

AD/BE =AF/BF

R/r = AF / (AF - sqrt(R^2+r^2))

R(AF - sqrt(R^2+r^2)) = r·AF

R·AF - R·sqrt(R^2+r^2) = r·AF

(R-r)AF = R·sqrt(R^2+r^2)

AF = R·sqrt(R^2+r^2) / (R-r)

Las rectas tangentes a la circunferencia de radio R pasan por puntos

(Xo, sqrt(R^2-xo^2)) y su vector director es perpendicular luego (sqrt(R^2-xo^2), -xo)

su ecuación paramétrica será

x = xo + t·sqrt(R^2-xo^2)

y = sqrt(R^2-xo^2) - t·xo

Debemos calcular la que pasa por el punto F=(R·sqrt(R^2+r^2) / (R-r), 0), eso nos da estas dos ecuaciones

R·sqrt(R^2+r^2) / (R-r) = xo + t·sqrt(R^2-xo^2)

0 = sqrt(R^2-xo^2) - t·xo

de esta segunda obtenemos

t^2·xo^2 = R^2 - xo^2

t = sqrt(R^2-xo^2) / xo

llevamos este valor a la primera

R·sqrt(R^2+r^2) / (R-r) = xo + [sqrt(R^2-xo^2) / xo]·sqrt(R^2-xo^2)

R·sqrt(R^2+r^2) / (R-r) = xo + (R^2-xo^2) / xo

xo·R·sqrt(R^2+r^2) / (R-r) = xo^2 + R^2 - xo^2

xo = R(R-r) / sqrt(R^2+r^2)

Luego el punto D es

(R(R-r) / sqrt(R^2+r^2), sqrt(R^2- [R(R-r)]^2 / (R^2+r^2))

¡Uff, no se entiende!

$$\begin{align}&D=\left(\frac{R(R-r)}{\sqrt{R^2+r^2}}\;,\sqrt{R^2-\frac{R^2(R-r)^2}{R^2+r^2}}  \right) =\\ &\\ &\left(\frac{R(R-r)}{\sqrt{R^2+r^2}}\;,\sqrt{\frac{R^4+R^2r^2-R^4-R^2r^2+2R^3r}{R^2+r^2}}  \right)=\\ &\\ &\left(\frac{R(R-r)}{\sqrt{R^2+r^2}}\;,R \sqrt{\frac{2Rr}{R^2+r^2}}  \right)\\ & \end{align}$$

Con esto la distancia DF es

$$\begin{align}&\sqrt{\left(\frac{R(R-r)}{\sqrt{R^2+r^2}}-\frac{R·\sqrt{R^2+r^2}}{R-r}\right)^2+\frac{R^2·2Rr}{R^2+r^2}}=\\ &\\ &\\ &\sqrt{\left(\frac{R(R-r)^2-R(R^2+r^2)}{(R-r)\sqrt{R^2+r^2}}\right)^2+\frac{2R^3r}{R^2+r^2}}=\\ &\\ &\\ &\sqrt{\left(\frac{R^3+Rr^2-2R^2r-R^3-Rr^2)}{(R-r)\sqrt{R^2+r^2}}\right)^2+\frac{2R^3r}{R^2+r^2}}=\\ &\\ &\\ &\sqrt{\frac{4R^4r^2}{(R-r)^2(R^2+r^2)}+\frac{2R^3r}{R^2+r^2}}=\\ &\\ &\\ &\sqrt{\frac{4R^4r^2+2R^3r(R-r)^2}{(R-r)^2(R^2+r^2)}}=\\ &\\ &\\ &\sqrt{\frac{4R^4r^2+2R^5r+2R^3r^3-4R^4r^2}{(R-r)^2(R^2+r^2)}}=\\ &\\ &\\ &\sqrt{\frac{2R^5r+2R^3r^3}{(R-r)^2(R^2+r^2)}}=\\ &\\ &\\ &\sqrt{\frac{2R^3r(R^2+r^2)}{(R-r)^2(R^2+r^2)}}=\\ &\\ &\frac{R \sqrt{2Rr}}{R-r}\\ &\\ &\end{align}$$

Y por la semejanza de los triángulos ADF y BEF tenemos

AD/BE = DF/EF

AD/BE = DF/(DF - DE)

AD(DF-DE) = DF·BE

AD·DF - AD·DE = DF·BE

-AD·DE = DF(BE-AD)

DE = DF(AD-BE)/AD

$$DE = \frac{R·\sqrt{2Rr}}{R-r}·\frac {R-r}{R} = \sqrt{2Rr}$$

Y esa es la distancia de segmento de la tangente entre las dos circunferencias.

No sé qué estarás estudiando, puede que con geometría proyectiva, razones dobles, ejes radicales, etc sea un problema fácil, pero de esa parte de la geometría apenas me acuerdo.

He hecho una pequeña prueba con el dibujo, los radios eran 2 y 1.16487

La tangente se trazó a ojo, puede tener algún fallo.

La formula dice

tangente = DE = 2.157934197

Y la distancia de la tangente del dibujo es 2.16784

Está muy pero que muy bien, un error mínimo para una tangente trazada a mano que confirma la veracidad de la fórmula.

También te pido que si sabes una forma sencilla de hacerlo me lo digas.