Ayuda urgente por favor!. Ciclo intro pregunta de examen..

Podrías explicarme mejor cuál es el recorrido del objeto. Es dando la vuelta por la elipse, es perpendicular a la elipse hasta el centro.
¿La fuerza es un vector no? La componente en x es y y la componente en y es -x. ¿Es eso, no?
El aréa de la elipse es PI·a·b. Pero no sabía que hubiera un teorema. Supongo que se hará por cálculo integral. ¿Es así como debo demostrarlo?

2)Me olvidaba también mandame la demostración del teorema de l área de la elipse.
Saludos.

El problema decía así, pero tuve la misma duda que tú entonces le pregunté al profe y me dijo que el recorrido es tocando los puntos de la elipse, en otras palabras apegado en su curva. Por supuesto que la fuerza es otro vector y las componentes que te dí son correctas.
Conozco el área de la elipse por teoría pi.a.b, me equivoque en decir que era un teorema, más sería una fórmula ¿verdad?.
Si tú me dices que puedes demostrar por medio del calculo integral .Vale.
Más no sé si te llego un problema con 6 preguntas del mismo tema, creo que me excedí sino te la mando en 2 partes o no sé dime tú.Si no te acuerdas los problemas, son en los que te pido que calcules las derivadas de las funciones inversas.
Atte: F.P.D.L.

El trabajo que efectúa un objeto moviéndose en un campo de fuerza es la integral de línea de ese campo de fuerza a través de la linea descrita.
Las integrales de llínea se calculan haciendo un parametrización de la curva descrita
curva(t) = (f(t), g(t)) y luego mediante la fórmula
$de linea de Xdx + Ydy = $X(f(t)) f'(t) + Y(g(t)) g'(t) dt
La mejor parametrización existente par la elipse es (f(t),g(t))=(acost, bsent)
f '(t) = -asent
g'(t) = bcost
en el intervalo [0,2PI]
(-1/2)$bsent(-asent) + (-acost)bcost en x€[0,2pi] = ab/2 $sen^2(t)+cos^t dt en x€[0,pi]=
ab/2 $1dt en x€[0,2pi] = abx/2 en x€[0,2pi] = PI·a·b
Luego el trabajo realizado es el área de la elipse.
Ya continuaré, tengo que dormir algo.

La verdad que no entiendo el concepto de parametrización, supuongo que son cordenadas polares, por ejemplo en el caso de una circunferencia seria x=rcost ; y=rsent.
¿Quizás se puede entender a la parametrización como una forma de representar formas de POR y Y tal que cumplan su ecuación verdad? Si fuese así entonces mencióname otra parametrización de la elipse no de la que se conoce que es más sencilla; sólo para ver.
¿Ahora el concepto de integrales de línea no lo entiendo'?
Yo entindo como si fuese cualquier integral común que te arroja cómo resultado el área de su respectiva gráfica que en este caso sería la gráfica F vs distancia.
No entiendo cómo llegas a la siguiente relación, que más bien sería una fórmula.
$de linea de Xdx + Ydy = $X(f(t)) f'(t) + Y(g(t)) g'(t) dt.
Lo que yo puedo comprender es que POR, y Y son las componentes de F.
También dx sería una diferencial de por, f(t) sería una función de la cordenada por para cualquier instante de tiempo.
Responder por favor esta duda cuando antes.
Atte:F.P.D.L.

No, una parametrización de una función y = f(x) es una función g
g : I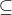 R ----------> J RxR
t -------------> (gx(t), gy(t))
tal que (gx(t), gy(t)) = (x, f(x))
Lo que se hace es recorrer la curva mediante la variable t que no tiene porque ser el ángulo, puede ser la distancia al origen, el tiempo o cualquier otra cosa.
En particular la función (t, f(t)) es una parametrización trivial de f, aunque hay casos más interesantes.
Por eso, para la parte superior de la elipse nos puede servir la parametrización
(t, (b/a)sqrt(a^2 - t^2)) con t€[-a, a]
Y para la negativa
(t, - (b/a)sqrt(a^2 - t^2)) con t€[a, -a]
No se pueden unir en una a no ser que modifiquemos el dominio de t de una pra que no coincidad y por ende la función gy(t). Pero para los efectos de recorrer la curva calculando el trabajo, que es el problema que nos plantean, nos valen esa dos parametrizaciones encadenadas una tras otra.
Pero es mucho más sencillo recorrer la elipse con la parametrización
g(t) = (acost, bsent) con t€[0,2PI]
Nótese que esta t no es el ángulo de las coordenadas polares.
Esto lo pone en la wikipedia y es verdad. Lo digo porque experimenté en mis propias carnes las consecuencias de pensar que eran el mismo y me volví loco cuando la integral polar del área de la elipse me daba PI(a^2+b^2) en lugar de PIab por más que repasaba donde podía estar el fallo y no lo ancontraba.
¿Qué quiero decir con eso? Que si tomo un segmento con ángulo t, el corte con la elipse no será (acost, b sent) como podía muy bien pensar uno. Sin embargo la parametrización sirve para recorrer la elipse con una velocidad distinta que la que lo haría una parametrización acorde con el ángulo polar.
Espero no haberme enrollado mucho, ahora tengo que irme pero te dejo esto.

Muy bien en tu respuesta, pero no me has respondido una de mis preguntas, como llegas a establecer lo siguiente.
$de linea de Xdx + Ydy = $X(f(t)) f'(t) + Y(g(t)) g'(t) dt.
Sólo lo que entiendo es que estarías calculando la integral de una curva cerrada., pero cómo llegas a de cir que se cumple aquello.
Atte:F.P.D.L.

Si que me perdí por las ramas. Pero este problema es raro desde el principio. Si te ponen este problema lo normal es que hubieras dado ya la teoría sobre las integrales de línea, porque es la forma como se resuelven estos problemas. Por eso yo te lo resolví al principio suponiendo eso y de acuerdo con la teoría que en cualquier libro te puedan dar sobre estas integrales. Ahora resulta que ni sabes lo que es una integral de línea ni un a parametrización. No entiendo entonces porque se ha adelantado el profesor al poner este problema.
Las integrales de línea surgen precisamente de este problema, el de calcular el trabajo de desplazamiento de un objeto por un campo de fuerzas.
Lo de
$de linea de Xdx + Ydy = $X(f(t)) f'(t) + Y(g(t)) g'(t) dt.
Es por teoría, la demostración esta fuera del alcance porque te falta la base y te irían surgiendo nuevas dudas.
Vamos a abordar el problema comenzando de cero, olvidando la basta teoría que existe al respecto.
El trabajo en cada intervalo del recorrido es el producto escalar del vector desplazamiento por el vector de la fuerza. Si el vector desplazamiento fuese constante eso sería una simple multiplicación de espacio por fuerza. Pero en este caso, el vector desplazamiento cambia constantemente, por eso el trabajo será la suma de los trabajos en los intervalos infinitesimales que constituyen el recorrido. Eso es una integral precisamente.
Nos falta calcular cuál es el trabajo en cada intervalo. Cuando la longitud del intervalo tiende a cero el vector que une el punto inicial con el final tiende en dirección y sentido al vector de la recta tangente en ese punto, el cual se obtiene derivando la función de desplazamiento, la elipse en nuestro caso.
Por más que lo he intentado, es muy complicado hacer los productos escalares e integrarlos a partir de la ecuación canónica de la elipse. Así que queramos o no, vamos a hacer la parametrización cubierta o encubierta, con lo que los puntos de la elipse serán:
(acost, bsent) para t€[0, 2PI]
Vemos que en efecto
a^2cos^2(t) / a^2 + b^2sen^2(t) / b^2 = cos^2(t)+sen^2(t) = 1
Luego los puntos (acost, bsent) verifican la ecuación de la elipse. Y con t entre 0 y 2PI recorremos todos los puntos de ella.
Llamemos h al incremento de t en un punto al recorrer la elipse
Pasamos del punto (acost, bsent) al punto (acos(t+h), bsen(t+h))
La coordenada por del vector desplazamiento es acos(t+h) - acos(t)
La coordenada y será bsen(t+h) - bsen(t)
El producto escalar de la fuerza por el deaplazamiento en ese intervalo es
-(1/2) (y, -x) · (acos(t+h) - acos(t), bsen(t+h) - bsen(t)) =
-(1/2) (bsen(t), -acos(t)) · (acos(t+h)-acos(t), bsen(t+h)-bsen(t)) =
Usamos la táctica de multiplicar y dividir por h
-(h/2) (bsen(t), -acos(t)) · ([acos(t+h)-acos(t)]/h, [bsen(t+h)-bsen(t)]/h) =
Cuando h-->0 en el segundo vector tiende a sendas derivadas
=-(h/2) (bsen(t), -acos(t)) · (acos'(t), bsen'(t))=
Efectuamos dichas derivadas
= -(h/2) (bsen(t), -acos(t)) · (-asen(t), b cos(t)) =
Efectuamos el producto escalar.
= -(h/2) (-absen^2(t) - abcos^2(t)) =
= abh/2 (sen^2(t)+cos^2(t))
= abh/2
La suma de todos estos trabajos entre 0 y 2PI cuando h -->0 es una integral, la siguiente:
$(1/2)abdt en t€[0,2PI] = (1/2)abt en t€(0,2PI) (1/2)ab(2PI - 0) = PI·a·b
Que es el área de la elipse.
Desde luego que se hace raro tener que explicar todo esto cuando con la teoría no sería necesario.