Dudas respecto a problemas de circunferencias y cuadriláteros inscriptibles
Buen día experto, necesito ayuda con estos problemas de circunferencias y cuadriláteros inscriptibles, ya resolví casi todos falta solo estos, por favor ayudenme, solo enumerenme los pasos de cada uno, no tan explicado que yo me doy cuenta fácilmente
Esta es la imagen de los 4 problemas que me faltan
http://imageshack.us/photo/my-images/8/circunycuadriins.jpg/
Según veo el ultimo debe inscribirse en una circunferencia...
Esta es la imagen de los 4 problemas que me faltan
http://imageshack.us/photo/my-images/8/circunycuadriins.jpg/
Según veo el ultimo debe inscribirse en una circunferencia...
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
1
Ya miré el problema que estaba en el tablón y es realmente difícil. Sobre todo porque de los dibujos no he podido deducir cual es el orden de construcción de alguno de ellos. Y si no se sabe cuál es el orden de construcción mal puede resolverse un problema geométrico de estos. Yo puedo intentarlo pero tendré que preguntarte varias cosas. Empieza por decirme lo que puedas del orden de construcción, sobre todo en el 3 y 4 que no tengo ni idea. También dime en que contexto están estos problemas, que tipo de geometría se estudia. Porque por geometría euclidea (con coordenadas por e y) se resuelve lo que te echen, pero no creo que sea eso lo que se espera que hagamos.
Quedo a la espera de que me des un a luz para ponerme en marcha.
Quedo a la espera de que me des un a luz para ponerme en marcha.

Todo es geometría euclidea(la más fácil)
Gráfica 1
Dibujas una semicircunferencia TOQUE(O centro), luego trazas las rectas tangentes que son PA Y QA, luego se traza la recta secante QB intersectando a la circunferencia en C;luego desde el centro O, trazar una recta hasta B de modo que sea perpendicular a AB;luego trazar CQ, y como ves esos son los ángulos m<BAP=x , m<APC=50º
Gráfica 2
Dibujar una circunferencia(se prefiere dibujar 1/4 de ella), tomar como centro del cuadrado a formar un punto del cuarto de circunferencia;desde el centro de la circunferencia, trazar el radio y su prolongación, de modo que este sea el lado del cuadrado a formar... eso se aprecia el la figura...
Gráfica 3
Graficar una semicircunferencia con diámetro AOB (O centro), entre OB se haya el punto H, desde ahí trazar una perpendicular hasta DE, cortando a la circunferencia en C.desde DE, trazar las rectas tangentes DP y DQ;luego trazar la recta HQ.Los ángulos son :
m<DPC=theta ; m<DQC=alpha ; m<QHB=x
grafica 4
Es un simple triangulo,donde AB=CD(ya esta expresado con el punto grueso dibujado);m<BAD=2x ; m<ABD=4x ; m<CBD=x.Aqui segun veo debe inscribirse de alguna manera en una circunferencia,porque de eso trata el tema
Nota: m<ABC :medida del angulo ABC,es decir vulgarmente una parte del angulo B,segun la grafica
Espero hallas entendido las gráficas, espero tu pronta respuesta, gracias!
Gráfica 1
Dibujas una semicircunferencia TOQUE(O centro), luego trazas las rectas tangentes que son PA Y QA, luego se traza la recta secante QB intersectando a la circunferencia en C;luego desde el centro O, trazar una recta hasta B de modo que sea perpendicular a AB;luego trazar CQ, y como ves esos son los ángulos m<BAP=x , m<APC=50º
Gráfica 2
Dibujar una circunferencia(se prefiere dibujar 1/4 de ella), tomar como centro del cuadrado a formar un punto del cuarto de circunferencia;desde el centro de la circunferencia, trazar el radio y su prolongación, de modo que este sea el lado del cuadrado a formar... eso se aprecia el la figura...
Gráfica 3
Graficar una semicircunferencia con diámetro AOB (O centro), entre OB se haya el punto H, desde ahí trazar una perpendicular hasta DE, cortando a la circunferencia en C.desde DE, trazar las rectas tangentes DP y DQ;luego trazar la recta HQ.Los ángulos son :
m<DPC=theta ; m<DQC=alpha ; m<QHB=x
grafica 4
Es un simple triangulo,donde AB=CD(ya esta expresado con el punto grueso dibujado);m<BAD=2x ; m<ABD=4x ; m<CBD=x.Aqui segun veo debe inscribirse de alguna manera en una circunferencia,porque de eso trata el tema
Nota: m<ABC :medida del angulo ABC,es decir vulgarmente una parte del angulo B,segun la grafica
Espero hallas entendido las gráficas, espero tu pronta respuesta, gracias!
Si, el dos era sencillo y ya lo había medio resuelto. Lo que pasa es que no sé si es el método que te exigirán.
Tomo como ejes de coordenadas las rectas AH y CD, el punto (0,0) es D.
Marco como punto H el centro de la circunferencia, sus coordenadas las llamaré (h, 0)
Los puntos C y E están en la circunferencia, luego equidistan del centro que es H
Llamando L al lado del cuadrado tenemos, que respecto a los ejes cartesianos que nos hemos dado:
Las coordenadas de C son (0, L)
las coordenadas de E son (-L/2, L/2)
las coordenadas de H eran (h, 0)
Cuadrado de la distancia HC = h^2 + L^2
Cuadrado de la distancia HE = (h + L/2)^2 + (L/2)^2 = h^2 + (L^2)/4 + hL + (L^2)/4 =
h^2 - hL + (L^2) / 2
igualamos los cuadrados de las distancias HC y HE
h^2 + L ^2 = h^2 + hL + (L^2)/2
L^2 = hL + (L^2)/2
hL = (L^2)/2
h = L/2
Ahora dibuja y fíjate en el triángulo CDH. El lado DH mide lo que acabamos de calcular L/2 y el lado CD mide L.
DH/CD = tg del angulo en C
DH/CD = (L/2) / L = 1/2
arctg(1/2) = 26,565051
El ángulo en H de ese triángulo es el complementario = 90 - 26,565051 = 63,434949
Este angulo H es el de sector FHC. Para calcular el del sector EHC hay que restar el ángulo FHE.
Trazando el radio hasta E y bajando desde ahí se forma otro triángulo rectángulo. El cateto opuesto tiene L/2 de altura. El adyacente tiene L/2 a la izquierda y otros L/2 a la derecha del punto origen por los cálculos que hicimos antes, luego mide L.
La tangente del angulo es como antes 1/2 y el arctg es 26,565051 tal como habíamos calculado antes.
Entonces y terminando ya, el ángulo exacto del sector EHC = 63,434949 - 26,565051 = 36,869898
Que es más o menos el ángulo 37 que indica la solución b.
Y esto es todo. Los demás los tengo que estudiar y no sé si podré. Además no sé si este método que he usado te sirve. Házmelo saber. Y dentro nada a dormir, que en España ya son las 5 de la mañana.
Tomo como ejes de coordenadas las rectas AH y CD, el punto (0,0) es D.
Marco como punto H el centro de la circunferencia, sus coordenadas las llamaré (h, 0)
Los puntos C y E están en la circunferencia, luego equidistan del centro que es H
Llamando L al lado del cuadrado tenemos, que respecto a los ejes cartesianos que nos hemos dado:
Las coordenadas de C son (0, L)
las coordenadas de E son (-L/2, L/2)
las coordenadas de H eran (h, 0)
Cuadrado de la distancia HC = h^2 + L^2
Cuadrado de la distancia HE = (h + L/2)^2 + (L/2)^2 = h^2 + (L^2)/4 + hL + (L^2)/4 =
h^2 - hL + (L^2) / 2
igualamos los cuadrados de las distancias HC y HE
h^2 + L ^2 = h^2 + hL + (L^2)/2
L^2 = hL + (L^2)/2
hL = (L^2)/2
h = L/2
Ahora dibuja y fíjate en el triángulo CDH. El lado DH mide lo que acabamos de calcular L/2 y el lado CD mide L.
DH/CD = tg del angulo en C
DH/CD = (L/2) / L = 1/2
arctg(1/2) = 26,565051
El ángulo en H de ese triángulo es el complementario = 90 - 26,565051 = 63,434949
Este angulo H es el de sector FHC. Para calcular el del sector EHC hay que restar el ángulo FHE.
Trazando el radio hasta E y bajando desde ahí se forma otro triángulo rectángulo. El cateto opuesto tiene L/2 de altura. El adyacente tiene L/2 a la izquierda y otros L/2 a la derecha del punto origen por los cálculos que hicimos antes, luego mide L.
La tangente del angulo es como antes 1/2 y el arctg es 26,565051 tal como habíamos calculado antes.
Entonces y terminando ya, el ángulo exacto del sector EHC = 63,434949 - 26,565051 = 36,869898
Que es más o menos el ángulo 37 que indica la solución b.
Y esto es todo. Los demás los tengo que estudiar y no sé si podré. Además no sé si este método que he usado te sirve. Házmelo saber. Y dentro nada a dormir, que en España ya son las 5 de la mañana.
El problema 1 no tiene ese orden de ejecución.
Al final hablas de trazar CQ cuando eso ya se había hecho antes al trazar QB.
También dices: luego desde el centro O, trazar una recta hasta B de modo que sea perpendicular a AB. Pero no se puede elegir el tipo de recta. A, B, O ya existían antes, simplemente es una recta que une puntos ya fijados y no puede elegirse tal que haga tal cosa porque es única.
Déjame que te explique como creo yo que sería. Es que sino tampoco le encuentro explicación a que ese ángulo mida 50º, o bien estaba muy bien elegido el punto A origen de todo o bien se hace que ese angulo sea 50º a propósito.
Vale, semicircunferencia TOQUE con O el centro. Se trazan tangentes desde A, el cual está a la misma altura que QUE para que una tangente sea en QUE y la otra es en el punto P. Se traza una recta por P de modo que forme 50º con AP. Esa recta corta a la semicircunferencia en C. Se traza una recta que pase por C y Q. Y ahora tengo la duda de si la recta que parte de O se hace de modo que sea paralela a AQ o se hace para que sea perpendiculas a PC.
Una vez resuelta esa duda donde se corten estas dos últimas rectas es B y se traza BA.
Otra posibilidad es que PC se construya paralela paralela a TQ, pero entonces ya te decía que A debía estar milimetricamente calculado para que el ángulo fuese 50º.
Pues eso, que son muchas las dudas respecto al proceso de construcción y así no se puede poner uno a resolver sin saber si tiene sentido lo que hace. ¿Y estos problemas no tendrán un enunciado completo que describa el proceso?
Al final hablas de trazar CQ cuando eso ya se había hecho antes al trazar QB.
También dices: luego desde el centro O, trazar una recta hasta B de modo que sea perpendicular a AB. Pero no se puede elegir el tipo de recta. A, B, O ya existían antes, simplemente es una recta que une puntos ya fijados y no puede elegirse tal que haga tal cosa porque es única.
Déjame que te explique como creo yo que sería. Es que sino tampoco le encuentro explicación a que ese ángulo mida 50º, o bien estaba muy bien elegido el punto A origen de todo o bien se hace que ese angulo sea 50º a propósito.
Vale, semicircunferencia TOQUE con O el centro. Se trazan tangentes desde A, el cual está a la misma altura que QUE para que una tangente sea en QUE y la otra es en el punto P. Se traza una recta por P de modo que forme 50º con AP. Esa recta corta a la semicircunferencia en C. Se traza una recta que pase por C y Q. Y ahora tengo la duda de si la recta que parte de O se hace de modo que sea paralela a AQ o se hace para que sea perpendiculas a PC.
Una vez resuelta esa duda donde se corten estas dos últimas rectas es B y se traza BA.
Otra posibilidad es que PC se construya paralela paralela a TQ, pero entonces ya te decía que A debía estar milimetricamente calculado para que el ángulo fuese 50º.
Pues eso, que son muchas las dudas respecto al proceso de construcción y así no se puede poner uno a resolver sin saber si tiene sentido lo que hace. ¿Y estos problemas no tendrán un enunciado completo que describa el proceso?

Bueno he resuelto la numero 2, y obtengo mEC=37º, por trazos y descubro un angulo recto y luego dos ecuaciones ... es correcto
En la 1, la información es esa no hay más, no habla de paralelas, eso se tendría que demostrar, pero lo he resuelto y obtengo x=53º
La 3 simplemente todas esas rectas pasan por P y QUE que son puntos de tangencia, y según veo quizás x=37º
La 4 es obvio que debe inscribirse en una circunferencia, pero antes supongo que debo adaptar esa figura como un cuadrilátero, intente resolverlo, pero me falta algunas cosas, aun así veo que se obtendrá x=22.5º,¿cómo?
La forma de resolverlo son con trazos, y medir ángulos, nada más.
Y estos ejercicios son de liceo, muy fácil... Ojala puedas resolverlos... quiero comprobar mis resultados
En la 1, la información es esa no hay más, no habla de paralelas, eso se tendría que demostrar, pero lo he resuelto y obtengo x=53º
La 3 simplemente todas esas rectas pasan por P y QUE que son puntos de tangencia, y según veo quizás x=37º
La 4 es obvio que debe inscribirse en una circunferencia, pero antes supongo que debo adaptar esa figura como un cuadrilátero, intente resolverlo, pero me falta algunas cosas, aun así veo que se obtendrá x=22.5º,¿cómo?
La forma de resolverlo son con trazos, y medir ángulos, nada más.
Y estos ejercicios son de liceo, muy fácil... Ojala puedas resolverlos... quiero comprobar mis resultados
¡Caramba, prefiero que me pongan unas integrales racionales con raíces complejas múltiples que esto! No sé que quieres decir con resolver con trazos. No sé si di esa teoría, que en todo caso tendría olvidada por completo porque la geometría no la he tocado tan apenas.
Pues ya intentaré algo. Dame buena cantidad de tiempo. Y ahora si que me voy a dormir de verdad.
Pues ya intentaré algo. Dame buena cantidad de tiempo. Y ahora si que me voy a dormir de verdad.
Sigo con los problemas y como no sé qué métodos utilizar haré lo que pueda aunque creo que ehora voy a pasarme algún pueblo. Me vendría muy bien que me dijeras como has resuelto esta clase de problemas o ya sería el sumun mandarme el escaneado del libro del tema este.
Ahora me podré con el cuatro.
Lo primero es escribir los ángulos que quedan
ADB = 180º - 6x
BDC = 6x
DCB = 180º - 7x
Tenemos tres triángulos el grande ABC y los internos ABD y BCD
En cada uno de ellos vamos a aplicar el teorema de los senos. Teniendo en cuenta que
AB=DC y que
sen a = sen (180-a)
quedan estas tres igualdades en virtud de ese teorema:
(AD+AB) / sen x = BC / sen 2x = AB / sen 7x
AD /sen 4x = BD / sen 2x = AB / sen 6x
AB / sen x = BC / sen 6x = BD / sen 7x
Tomemos la segunda igualdad de la primera línea
BC / sen 2x = AB / sen 7x ==> BC / AB = sen 2x / sen 7x
Y tomando la segunda igualdad de la tercera
AB / sen x = BC / sen 6x ==> BC / AB = sen 6x / sen x
Igualando BC / AB en ambas tenemos
sen 2x / sen 7x = sen 6x / sen x ==>
sen 2x · sen x = sen 6x · sen 7x ==>
sen 2x · sen x - sen 6x · sen 7x = 0
Es esta una ecuación prácticamente irresoluble, pero estamos en la era de los ordenadores y no nos cuesta nada hacer la gráfica y que ella misma nos de las soluciones.
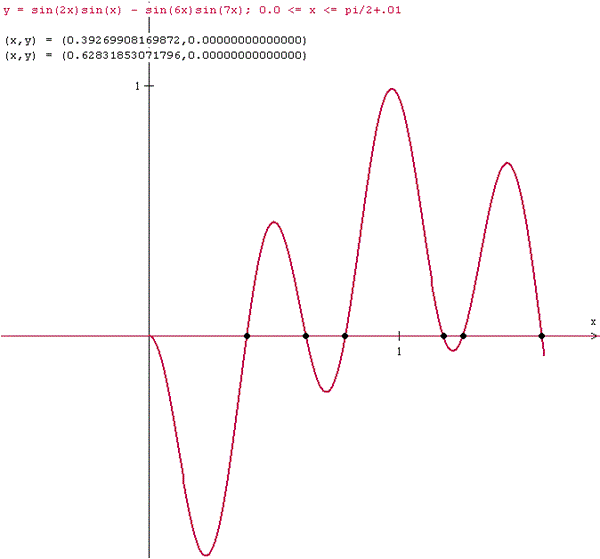
Estas respuestas están expresadas en radianes. Donde PI radianes = 180º
Tomando el triángulo ABC tenemos que el ángulo en A es 2x y en B es 5x, entre los dos 7x, luego los tres ángulos suman al menos 7x.
Es decir 7x <PI ==> x < PI/7 = 0,4487989
Y de todas las soluciones de la gráfica, la única que sirve es la primera, la segunda ya se pasa. Redondeando algo tenemos:
x =0,3927
Y esto expesado en grados es
0,3927·180 / PI = 22,5º
Luego la respuesta correcta del cuatro es la c
Ahora tengo que hacer otras cosas pero te dejo ya este resuelto y no sé si podré con el 3, no lo he mirado a fondo pero creo que tampoco veía muy claro el orden de ejecución.
Ahora me podré con el cuatro.
Lo primero es escribir los ángulos que quedan
ADB = 180º - 6x
BDC = 6x
DCB = 180º - 7x
Tenemos tres triángulos el grande ABC y los internos ABD y BCD
En cada uno de ellos vamos a aplicar el teorema de los senos. Teniendo en cuenta que
AB=DC y que
sen a = sen (180-a)
quedan estas tres igualdades en virtud de ese teorema:
(AD+AB) / sen x = BC / sen 2x = AB / sen 7x
AD /sen 4x = BD / sen 2x = AB / sen 6x
AB / sen x = BC / sen 6x = BD / sen 7x
Tomemos la segunda igualdad de la primera línea
BC / sen 2x = AB / sen 7x ==> BC / AB = sen 2x / sen 7x
Y tomando la segunda igualdad de la tercera
AB / sen x = BC / sen 6x ==> BC / AB = sen 6x / sen x
Igualando BC / AB en ambas tenemos
sen 2x / sen 7x = sen 6x / sen x ==>
sen 2x · sen x = sen 6x · sen 7x ==>
sen 2x · sen x - sen 6x · sen 7x = 0
Es esta una ecuación prácticamente irresoluble, pero estamos en la era de los ordenadores y no nos cuesta nada hacer la gráfica y que ella misma nos de las soluciones.

Estas respuestas están expresadas en radianes. Donde PI radianes = 180º
Tomando el triángulo ABC tenemos que el ángulo en A es 2x y en B es 5x, entre los dos 7x, luego los tres ángulos suman al menos 7x.
Es decir 7x <PI ==> x < PI/7 = 0,4487989
Y de todas las soluciones de la gráfica, la única que sirve es la primera, la segunda ya se pasa. Redondeando algo tenemos:
x =0,3927
Y esto expesado en grados es
0,3927·180 / PI = 22,5º
Luego la respuesta correcta del cuatro es la c
Ahora tengo que hacer otras cosas pero te dejo ya este resuelto y no sé si podré con el 3, no lo he mirado a fondo pero creo que tampoco veía muy claro el orden de ejecución.
Aquí estoy de nuevo. He encontrado una demostración bastante más sencilla más sencilla para el segundo.
Dibuja la parte de abajo de la circunferencia por la izquierda y prolonga el segmento CD hasta cortar a la parte de abajo de la circunferencia en G. Desde G traza el segmento hasta E. Y desde E traza el segmento perpendicular a CD desde E hasta CD, pongamos que se cortan en H
Por la teoría, el ángulo central mide el doble que el ángulo inscrito correspondiente. Nos piden calcular el angulo central de EC y eso será el doble que el ángulo inscrito EGC.
El cálculo del ángulo EGC es muy sencillo. Su tangente será cateto opuesto entre cateto adyacente. El cateto opuesto mide medio lado del cuadrado = L/2. El adyacente mide un cuadrado y medio = 3L/2
tg(EGC) = (L/2) / (3L/2) = 1/3
ángulo EGC =arctg(1/3) = 18,434949º
sector EC = 2(ángulo EGC) = 18,434949 · 2 = 36,869898º
Dibuja la parte de abajo de la circunferencia por la izquierda y prolonga el segmento CD hasta cortar a la parte de abajo de la circunferencia en G. Desde G traza el segmento hasta E. Y desde E traza el segmento perpendicular a CD desde E hasta CD, pongamos que se cortan en H
Por la teoría, el ángulo central mide el doble que el ángulo inscrito correspondiente. Nos piden calcular el angulo central de EC y eso será el doble que el ángulo inscrito EGC.
El cálculo del ángulo EGC es muy sencillo. Su tangente será cateto opuesto entre cateto adyacente. El cateto opuesto mide medio lado del cuadrado = L/2. El adyacente mide un cuadrado y medio = 3L/2
tg(EGC) = (L/2) / (3L/2) = 1/3
ángulo EGC =arctg(1/3) = 18,434949º
sector EC = 2(ángulo EGC) = 18,434949 · 2 = 36,869898º
- Compartir respuesta
- Anónimo
ahora mismo
