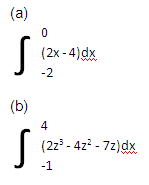Anónimo
Matemática para los negocios
Pregunta N° 1 (7 puntos)
Dada la función:
f(x) = x3/3 - 3x2/4 + 7x - 30
a) Hallar los puntos de la gráfica donde la recta tangente sea horizontal.
b) Evaluar V = 2f'( 5 + f(5) ) - 2f( 3f'(0) - 5f'(1) )
Caso N° 2 (7 puntos)
Un fabricante dispone de una capacidad instalada para producir hasta 2000 "agur" al mes. El "agur" es un dispositivo electrónico altamente especializado. En general todo lo que se produce se vende. Se sabe que la función utilidad U en $ que obtendrá de su producción dependerá del número de "agur" vendidos "a", de acuerdo a la expresión:
U(a) = 4800 a - 2a2
a) Calcular la producción para obtener máxima ganancia.
b) ¿En cuánto disminuiría su ganancia si se utiliza toda la capacidad instalada?
Pregunta N° 3 (6 puntos)
Calcular:
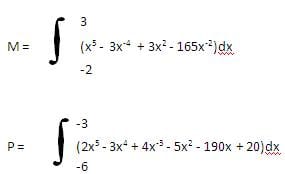
Dada la función:
f(x) = x3/3 - 3x2/4 + 7x - 30
a) Hallar los puntos de la gráfica donde la recta tangente sea horizontal.
b) Evaluar V = 2f'( 5 + f(5) ) - 2f( 3f'(0) - 5f'(1) )
Caso N° 2 (7 puntos)
Un fabricante dispone de una capacidad instalada para producir hasta 2000 "agur" al mes. El "agur" es un dispositivo electrónico altamente especializado. En general todo lo que se produce se vende. Se sabe que la función utilidad U en $ que obtendrá de su producción dependerá del número de "agur" vendidos "a", de acuerdo a la expresión:
U(a) = 4800 a - 2a2
a) Calcular la producción para obtener máxima ganancia.
b) ¿En cuánto disminuiría su ganancia si se utiliza toda la capacidad instalada?
Pregunta N° 3 (6 puntos)
Calcular:
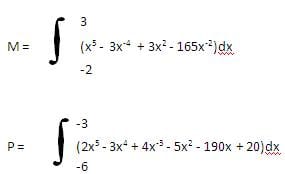
1 respuesta
Respuesta de rubeneduardo
2
Caso 1
a) Derivando para hallar la pendiente e igualando a cero (recta tangente horizontal)
df(x)/dx = x^2 - 3x/2 + 7 = 0 entonces 2x^2 - 3x + 14 = 0, analizando el discriminante (-3)^2 - 4(2)(14) < 0 no hay soluciones reales es decir no hay recta tangente horizontal.
b) Utilizo f(5) = 5^3/3 - 3*5^2/4 + 7*5 - 30 = 125/3 - 125/4 + 5 = (500 - 375)/12 + 5 = 125/12 + 5 = 185/12 f'(0) = 7 f'(1) = 13/2
V = 2f'(5 + 185/12) - 2f'( 3(7) - 5*13/2) = 2f'(245/12) - 2f'(-23/2) Finalmente reemplazo en los dos terminos 245/12 y -23/2 en la derivada y obtengo la respuesta ( no la resuelvo por ser algo extenso el calculo sin embargo si lo necesitas me dices)
Caso 2
a) Para obtener lo solicitado derivamos U'(x) = 4800 - 4a = 0 a = 1200 (nota que si derivamos otra vez obtengo -4 < 0 lo que indica que es un maximo relativo). Sin embargo debemos probar para a= 1200 y para a = 2000 para ver en que caso obtengo el máximo absoluto.
a= 1200 U = 2880000
a = 2000 U = 1600000
Entonces la solucion es a = 1200
b) Disminuiria 2880000 - 1600000 = 1280000
a) Derivando para hallar la pendiente e igualando a cero (recta tangente horizontal)
df(x)/dx = x^2 - 3x/2 + 7 = 0 entonces 2x^2 - 3x + 14 = 0, analizando el discriminante (-3)^2 - 4(2)(14) < 0 no hay soluciones reales es decir no hay recta tangente horizontal.
b) Utilizo f(5) = 5^3/3 - 3*5^2/4 + 7*5 - 30 = 125/3 - 125/4 + 5 = (500 - 375)/12 + 5 = 125/12 + 5 = 185/12 f'(0) = 7 f'(1) = 13/2
V = 2f'(5 + 185/12) - 2f'( 3(7) - 5*13/2) = 2f'(245/12) - 2f'(-23/2) Finalmente reemplazo en los dos terminos 245/12 y -23/2 en la derivada y obtengo la respuesta ( no la resuelvo por ser algo extenso el calculo sin embargo si lo necesitas me dices)
Caso 2
a) Para obtener lo solicitado derivamos U'(x) = 4800 - 4a = 0 a = 1200 (nota que si derivamos otra vez obtengo -4 < 0 lo que indica que es un maximo relativo). Sin embargo debemos probar para a= 1200 y para a = 2000 para ver en que caso obtengo el máximo absoluto.
a= 1200 U = 2880000
a = 2000 U = 1600000
Entonces la solucion es a = 1200
b) Disminuiria 2880000 - 1600000 = 1280000
Amigo muy interesante tu respuesta, pero ahora tengo una pregunta más muy similar a la anterior, aque me hubiera gustado comparar la prenta 3, espero si puedes apoyarme relizandolo
Pregunta N° 1 (6 puntos)
Dada la función:
f(x) = 14x - 8x3 - 5x2
a) Hallar los puntos de la gráfica donde la recta tangente sea horizontal.
b) Evaluar E = 2 f ' (0) - 3 f '(-10) - 5 f ' (8)
Pregunta N° 2 (4 puntos)
Hallar la primera derivada de:
E indique el valor de f ' (b+a)
Caso N° 1 (6 puntos)
Un productor dispone de 600 hectáreas aptas para sembrar. Se sabe que la ganancia total U en US$ que obtendrá de su producción dependerá del número de hectáreas sembradas por, de acuerdo a la expresión:
a) Calcular cuántas hectáreas debería sembrar para obtener máxima ganancia.
b) ¿En cuánto disminuiría su ganancia si sembrara las 600 hectáreas disponibles?
Pregunta N° 3 (4 puntos)
Calcular:
Pregunta N° 1 (6 puntos)
Dada la función:
f(x) = 14x - 8x3 - 5x2
a) Hallar los puntos de la gráfica donde la recta tangente sea horizontal.
b) Evaluar E = 2 f ' (0) - 3 f '(-10) - 5 f ' (8)
Pregunta N° 2 (4 puntos)
Hallar la primera derivada de:
E indique el valor de f ' (b+a)
Caso N° 1 (6 puntos)
Un productor dispone de 600 hectáreas aptas para sembrar. Se sabe que la ganancia total U en US$ que obtendrá de su producción dependerá del número de hectáreas sembradas por, de acuerdo a la expresión:
a) Calcular cuántas hectáreas debería sembrar para obtener máxima ganancia.
b) ¿En cuánto disminuiría su ganancia si sembrara las 600 hectáreas disponibles?
Pregunta N° 3 (4 puntos)
Calcular:
Ahí te va la explicación:
a) pregunta 1 f´(x) = 14 - 24x^2 - 10x = 0 que podemos escribir asi:
12x^2 + 5x - 7 = 0
12x -7
x 1
Por = 7/12 por = -1 (En estos puntos la recta tangente es horizontal, pues su derivada es igual a 0)
b) f´(0) = 14 f´(-10) = 14 - 24*(100) - 10(-10) = -2386 f´(8) = 14-24(64) -10(8) = -1602
E = 2(14) - 3(-2386) - 5(-1602)
Pregunta 2 falta detallar la función
Caso Nº1 (Falta la expresión)
Pregunta 3 ( Por la configuración de la maquina no carga la pregunta veo una por y no veo la pregunta por eso no respondí la pregunta 3 la vez anterior).
Voy a poner la pregunta como privada si puedes me las envías a [email protected]
a) pregunta 1 f´(x) = 14 - 24x^2 - 10x = 0 que podemos escribir asi:
12x^2 + 5x - 7 = 0
12x -7
x 1
Por = 7/12 por = -1 (En estos puntos la recta tangente es horizontal, pues su derivada es igual a 0)
b) f´(0) = 14 f´(-10) = 14 - 24*(100) - 10(-10) = -2386 f´(8) = 14-24(64) -10(8) = -1602
E = 2(14) - 3(-2386) - 5(-1602)
Pregunta 2 falta detallar la función
Caso Nº1 (Falta la expresión)
Pregunta 3 ( Por la configuración de la maquina no carga la pregunta veo una por y no veo la pregunta por eso no respondí la pregunta 3 la vez anterior).
Voy a poner la pregunta como privada si puedes me las envías a [email protected]
Acá te resuelvo las preguntas que faltan:
Pregunta 2
f´(x) = (b(x-a) - 1. (bx))(x-a)^2 = -ab/(x-a)^2
f´(a+b) = -ab/(b+a-a)^2 =-a/b
Caso Nº1
a) Para maximizar la funcion derivamos la expresion:
U´(x) = - 300000/x^2 +4 = 0 de donde x^2 = 75000 entonces x = 273.8 = 274 luego reemplazamos 274 y 600 en la expresion y comparamos:
x = 274 U= 2440.89
x = 600 U = 3150
En este caso el máximo relativo no coincide con el máximo absoluto la respuesta es por = 600 pues se obtiene una mayor ganancia.
b) En este caso no disminuiria pues con x= 600 obtengo la mayor ganancia.
Pregunta 3
Aplicando la formula general Integral (x^n) = x^(n+1)/(n+1) resolvemos la integral definida
a) 2x^2/2- 4x evaluado de -2 a 0 = x^2 - 4x evaluado de -2 a 0 = 0^2-4*0-((-2)^2-4(-2)) = -12
b) 2z^4/4 - 4*z^3/3 - 7z^2/2 evaluado de -1 a 4 = (4)^4/2 - 4*(4)^3/3 - 7*(4)^2/2 - ((-1)^4/2-4*(-1)^3/3 - /*(-1)^2/2)
Te hago notar el orden para evluar las integrales siempre primero el numero que va arriba y luego el de abajo pero a la hora de referirse verbalmente se menciona al revés del menor al mayor.
Pregunta 2
f´(x) = (b(x-a) - 1. (bx))(x-a)^2 = -ab/(x-a)^2
f´(a+b) = -ab/(b+a-a)^2 =-a/b
Caso Nº1
a) Para maximizar la funcion derivamos la expresion:
U´(x) = - 300000/x^2 +4 = 0 de donde x^2 = 75000 entonces x = 273.8 = 274 luego reemplazamos 274 y 600 en la expresion y comparamos:
x = 274 U= 2440.89
x = 600 U = 3150
En este caso el máximo relativo no coincide con el máximo absoluto la respuesta es por = 600 pues se obtiene una mayor ganancia.
b) En este caso no disminuiria pues con x= 600 obtengo la mayor ganancia.
Pregunta 3
Aplicando la formula general Integral (x^n) = x^(n+1)/(n+1) resolvemos la integral definida
a) 2x^2/2- 4x evaluado de -2 a 0 = x^2 - 4x evaluado de -2 a 0 = 0^2-4*0-((-2)^2-4(-2)) = -12
b) 2z^4/4 - 4*z^3/3 - 7z^2/2 evaluado de -1 a 4 = (4)^4/2 - 4*(4)^3/3 - 7*(4)^2/2 - ((-1)^4/2-4*(-1)^3/3 - /*(-1)^2/2)
Te hago notar el orden para evluar las integrales siempre primero el numero que va arriba y luego el de abajo pero a la hora de referirse verbalmente se menciona al revés del menor al mayor.